Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Комментарии (2)
Гусейханов М., Раджабов О. Концепции современного естествознания: Учебник
Глава 19. МЕТОДЫ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ
Невозмутимый строй во всем, созвучье полное в природе.
Ф. И. Тютчев
19.1. Системный метод исследования
В широком смысле слова под системным исследованием предметов и явлений окружающего нас мира понимают такой метод, при котором они рассматриваются как части и элементы определенного целостного образования. Эти части или элементы, взаимодействуя друг с другом, определяют новые, целостные свойства системы, которые отсутствуют у отдельных ее элементов. Главное, что определяет систему, — это взаимосвязь и взаимодействие частей в рамках целого. Для системного исследования характерно именно целостное рассмотрение, установление взаимодействия составных частей или элементов совокупности, несводимость свойств целого к свойствам частей.
Учение о системах возникло в середине XIX в., но приобрело особенно важное значение в XX в. Его иначе называют еще системным подходом к изучаемым объектам, или системным анализом.
Система — это такая совокупность элементов, или частей, в которой существует их взаимное влияние и взаимное качественное преобразование. С этой точки зрения современное естествознание приблизилось к тому, чтобы стать настоящей системой, потому что все его части ныне взаимосвязаны, в нем нет уже ни одной естественной науки в рафинированно чистом виде.
474
Под системой понимают совокупность компонентов и устойчивых, повторяющихся связей между ними. Процесс системного рассмотрения объектов широко применяется в самых различных областях общественных, естественных и технических наук, в практике социального планирования и управления в обществе, при решении комплексных социальных проблем, при подготовке и реализации разнообразных целевых программ.
Основными свойствами систем являются следующие:
- всеобщий характер, поскольку в качестве системы могут рассматриваться все без исключения предметы и явления окружающего мира;
- невещественность;
- внутренняя противоречивость (конкретность и абстрактность, целостность и дискретность, непрерывность и прерывность);
- способность к взаимодействию;
- упорядоченность и целостность;
- устойчивость и взаимообусловленность.
Способность процессов и явлений мира образовывать системы, наличие систем, системного строения материальной действительности и форм ее познания получила название системности. Понятие системности отражает одну из характерных признаков действительности: способность вступать в такого рода взаимодействия, в результате которых образуются новые качества, не присущие исходным объектам взаимодействия.
Система — это множество объектов вместе с отношениями между объектами, между их свойствами, которые взаимодействуют между собой таким образом, что обусловливают возникновение новых, целостных, системных свойств. Для лучшего понимания природы систем рассмотрим их строение, структуру и классификацию.
Строение системы характеризуется теми компонентами, из которых она образована. Такими компонентами являются: подсистемы, части или элементы системы. Подсистемы составляют наибольшие части системы, которые обладают определенной автономностью, но в то же время они подчинены и управля-
475
ются системой. Элементами называют наименьшие единицы системы.
Структурой системы называют совокупность тех специфических взаимосвязей и взаимодействий, благодаря которым возникают новые целостные свойства, присущие только системе и отсутствующие у отдельных ее компонентов.
Классификация систем может производиться по самым разным основаниям деления. Прежде всего все системы можно разделить на материальные и идеальные. К материальным системам относится подавляющее большинство систем неорганического, органического и социального характера. Материальными системами называют их потому, что их содержание и свойства не зависят от познающего субъекта. Содержание и свойства идеальных систем зависят от субъекта. Наиболее простой классификацией систем является деление их на статические и динамические. Среди динамических систем обычно выделяют детерминистические и вероятностные системы. Такая классификация основывается на характере предсказания динамики поведения систем. По характеру взаимодействия с окружающей средой различают системы открытые и закрытые. Обычно выделяют те системы, с которыми данная система взаимодействует непосредственно и которые называют окружением или внешней средой системы. Все реальные системы в природе и обществе являются, как мы уже знаем, открытыми и, следовательно, взаимодействующими с окружением путем обмена веществом, энергией и информацией. Системы классифицируют также на простые и сложные. Простыми системами называют системы с небольшим числом переменных, взаимоотношения между которыми поддаются математической обработке и выведению универсальных законов. Сложная система состоит из большого числа переменных и большого количества связей между ними. Сложная система имеет свойства, которых нет у ее частей и которые являются следствием эффекта целостности системы.
Среди всех сложных систем наибольший интерес представляют системы с так называемой обратной связью. Пример: падение камня и кошки. Камень индифферентен по отношению
476
к нам, а кошка нет. В системе "кошка — человек" имеется обратная связь между воздействием и ее реакцией, которой нет в системе "камень — человек".
Если поведение системы усиливает внешнее воздействие, это называется положительной обратной связью, если же уменьшает внешнее воздействие — отрицательной обратной связью. Особый случай представляют гомеостатические обратные связи, которые действуют, чтобы свести внешнее воздействие к нулю. Пример: температура тела человека, которая остается постоянной благодаря гомеостатическим обратным связям.
Механизм обратной связи призван сделать систему более устойчивой, надежной и эффективной. В техническом, функциональном смысле понятие обратной связи означает, что часть выходной энергии аппарата или машины возвращается на вход. Механизм обратной связи делает систему принципиально иной, повышая степень ее внутренней организованности и давая возможность ее самоорганизации в данной системе.
Наличие механизма обратной связи позволяет дать заключение о том, что система преследует какие-то цели, т. е. что ее поведение целесообразно. Всякое целенаправленное поведение требует отрицательной обратной связи. Научное понимание целесообразности строилось на обнаружении в изучаемых предметах объективных механизмов целеполагания.
Возникновение и применение системного метода в науке знаменует значительно возросшую зрелость современного этапа его развития.
Преимуществами и перспективами системного метода исследования являются следующие:
1. Системный метод дает возможность раскрыть более
глубокие закономерности, присущие широкому классу взаимо
связанных явлений. Предмет этой теории составляет установ
ление и вывод тех принципов, которые справедливы для систем
в целом.
2. Фундаментальная роль системного метода заключается в
том, что с его помощью достигается наиболее полное выражение
единства научного знания. Это единство проявляется, с одной
477
стороны, во взаимосвязи различных научных дисциплин, которая выражается в возникновении новых дисциплин на "стыке" старых (физическая химия, химическая физика, биофизика, биохимия, биогеохимия и др.), а с другой — в появлении междисциплинарных направлений исследования (кибернетика, синергетика, экология и т. п.).
- Единство, которое выявляется при системном подходе к науке, заключается прежде всего в установлении связей и отношений между самыми различными по сложности организации, уровню познания и целостности охвата системами, с помощью которых отображаются рост и развитие нашего знания о природе. Чем обширнее система, чем сложнее она по уровню познания и структурной организации, тем больший круг явлений она в состоянии объяснить. Таким образом, единство знания находится в прямой зависимости от его системности.
- С позиций системности, единства и целостности научного знания становится возможным правильно подойти к решению таких проблем, как редукция, или сведение одних теорий естествознания к другим, синтез, или объединение кажущихся далекими друг от друга теорий, их подтверждение и опровержение данными наблюдений и экспериментов.
- Системный подход в корне подрывает прежние представления о естественно-научной картине мира, когда природа рассматривалась как простая совокупность различных процессов и явлений, а не тесно взаимосвязанных и взаимодействующих систем, различных как по уровню своей организации, так и по сложности.
Системный подход исходит из того, что система как целое возникает не каким-то мистическим и иррациональным путем, а в результате конкретного, специфического взаимодействия вполне определенных реальных частей. Именно вследствие такого взаимодействия частей и образуются новые интегральные свойства системы.
Таким образом, процесс познания природных и социальных систем может быть успешным только тогда, когда в них части и целое будут изучаться не в противопоставлении, а во взаимодействии друг с другом, анализ будет сопровождаться синтезом.
478
Вместе с тем представляются ошибочными взгляды сторонников философского учения холизма (от греч. holos— целое), которые считают, что целое всегда предшествует частям и всегда важнее частей. В применении к социальным системам такие принципы обосновывают подавление личности обществом, игнорирование его стремления к свободе и самостоятельности. На первый взгляд, может показаться, что концепция холизма о приоритете целого над частью согласуется с принципами системного метода, который также подчеркивает большое значение идей целостности, интеграции и единства в познании явлений и процессов природы и общества. Но при более внимательном знакомстве оказывается, что холизм преувеличивает роль целого в сравнении с частью, значение синтеза по отношению к анализу. Поэтому он является такой же односторонней концепцией, как атомизм и редукционизм. Системный метод избегает этих крайностей в познании мира. Именно вследствие взаимодействия частей образуются новые интегральные свойства системы. Но вновь возникшая целостность, в свою очередь, начинает оказывать воздействие на части, подчиняя их функционирование задачам и целям единой целостной системы.
19.2. Кибернетика - наука о сложных системах
Наука — это неустанная многовековая работа мысли свести посредством системы все познаваемые явления нашего мира.
А. Эйнштейн
Самым значительным шагом в формировании идеи системного метода было появление кибернетики как общей теории управления в технических системах, живых организмах и обществе. В рамках кибернетики впервые было ясно показано, что процесс управления с самой общей точки зрения можно рассматривать как процесс накопления, передачи и преобразования информации. Само же управление можно отобразить с помощью определенной последовательности точных предписаний — ал-
479
горитмов, посредством которых осуществляется достижение поставленной цели.
Наука, которая занимается исследованиями процессов управления сложными системами с обратной связью, получила название кибернетики (от греч. kybernetik— искусство управления). Она возникла на стыке математики, техники и нейрофизиологии, и ее интересует целый класс как живых, так и неживых систем, в которых существуют механизмы обратной связи. Основателем кибернетики считается американский математик Н. Винер, выпустивший в 1948 г. книгу "Кибернетика".
Кибернетика изучает способы связи и модели управления, и в этом исследовании ей понадобилось ввести понятие информации (от лат. informatio— ознакомление, разъяснение) как меры организованности системы в противоположность понятию энтропии как меры неорганизованности. Понятие информации имеет такое большое значение, что оно вошло в заглавие нового научного направления, возникшего на базе кибернетики — информатики (соединение слов информация и математика).
С повышением энтропии уменьшается информация (поскольку все усредняется) и, наоборот, понижение энтропии увеличивает информацию. Связь информации с энтропией свидетельствует и о связи информации с энергией. Энергия (от греч. energia— деятельность) характеризует общую меру различных видов движения и взаимодействия.
Информация характеризует меру разнообразия систем. Хотя информация и энергия относительно обособлены друг от друга, тем не менее они связаны между собой. Информация растет с повышением разнообразия системы. Одним из основных законов кибернетики является закон необходимого разнообразия: эффективное управление какой-либо системой возможно только в том случае, когда разнообразие управляющей системы больше разнообразия управляемой системы. Значит, чем больше мы имеем информации о системе, которой собираемся управлять, тем эффективнее будет проходить этот процесс.
Общее значение кибернетики обозначается в следующих направлениях:
480
- Философское значение — дает новое представление о мире, основанное на роли связи, управления, информации, организованности, обратной связи, целесообразности, вероятности.
- Социальное значение — дает новое представление об обществе как организованной целой системе.
- Общенаучное значение — дает новые понятия управления, методы исследования, формирует гипотезы о внутреннем составе и строении систем.
- Методологическое значение — изучая простые технические системы, выдвигает гипотезы о работе сложных систем (живых организмов, мышления людей).
- Техническое значение — создание ЭВМ, роботов, персональных компьютеров. ЭВМ и персональные компьютеры облегчают умственный труд, заменяя человеческий мозг в его наиболее простых и рутинных функциях. ЭВМ работают по принципу "да-нет", и этого оказалось достаточно для того, чтобы создать вычислительные машины, хотя и уступающие мозгу в гибкости, но превосходящие его по быстроте выполнения вычислительных операций. Если же будут построены не просто человекоподобные роботы, но и превосходящие его по уму, то это повод не только для радости, но и для беспокойства, связанного как с роботизацией самого человека, так и с проблемой возможного выхода машин из-под контроля людей и даже возможного порабощения ими человека.
19.3. Методы математического моделирования
Тот, кто хочет решать вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать измеримым то, что таковым, не является.
Г. Галилей
Выявление общего, существенного, присущего всем системам определенного рода производится наиболее общим приемом —
481
математическим моделированием. При математическом моделировании систем наиболее ярко проявляется эффективность единства качественных и количественных методов исследования, характеризующая магистральный путь развития современного научного познания.
Всякая сложная система, модель которой мы создаем, при своем функционировании подчиняется определенным законам — физическим, химическим, биологическим и др. Рассматриваются такие системы, для которых знание законов предполагает известные количественные соотношения, связывающие те или иные характеристики моделируемой системы. Модель создается для ответа на множество вопросов о моделируемом объекте. Интересуясь некоторыми аспектами функционирующей системы, изучают ее с определенных точек зрения. Направления изучения системы в значительной степени и определяет выбор модели. Опишем процесс построения математической модели сложной системы. Его можно представить состоящим из следующих этапов:
- Формулируются основные вопросы о поведении системы, ответы на которые мы хотим получить с помощью модели.
- Из множества законов, управляющих поведением системы, учитываются те, влияние которых существенно при поиске ответов на поставленные вопросы.
- В дополнение к этим законам, если необходимо, для системы в целом или отдельных ее частей формулируются определенные гипотезы о функционировании. Как правило, эти гипотезы правдоподобны в том смысле, что могут быть приведены некоторые теоретические доводы в пользу их принятия.
- Гипотезы, так же как и законы, выражаются в форме определенных математических соотношений, которые объединяются в некоторое формальное описание модели.
На этом заканчивается процесс построения математической модели. Дальше следует процесс исследования этих соотношений с помощью аналитических и вычислительных методов, приводящий в конечном итоге к отысканию ответов на предъявляемые модели вопросы. Разрабатывается или используется созданный
482
ранее алгоритм для анализа этой модели. Если модель и алгоритм не слишком сложны, то может оказаться возможным аналитическое исследование модели. В противном случае составляется программа, реализующая этот алгоритм на ЭВМ. После выполнения расчетов по модели на ЭВМ их результаты обязательно сравниваются с фактической информацией из соответствующей предметной области. Это сравнение необходимо для того, чтобы убедиться в адекватности модели, в том, что модельным расчетам можно верить, их можно использовать.
Если модель хороша, то ответы, найденные с ее помощью, как правило, бывают весьма близки к ответам на те же вопросы о моделируемой системе. Более того, в этом случае зачастую с помощью модели удается ответить и На некоторые ранее не ставившиеся вопросы, расширить круг представлений о реальной системе. Если же модель плоха, т. е. недостаточно адекватно описывает систему с точки зрения задаваемых ей вопросов, то она подлежит дальнейшему улучшению или замене. Возможны также ошибки в алгоритме, в программе для ЭВМ. Такие повторные просмотры продолжаются до тех пор, пока результаты расчетов не удовлетворят исследователя. Теперь модель готова к использованию. Критерием адекватности модели служит практика, которая и определяет, когда может закончиться процесс улучшения модели. Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную исходную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человечества.
Достоинствами метода математического моделирования является то, что модель представляет собой формализованную запись тех или иных законов природы, управляющих функционированием системы. Однако определенные трудности возникают при попытке построения математической модели очень сложной системы.
Существуют различные модели, используемые для описания сложных систем, такие как:
483
- дескриптивные (описательные), описывающие происходящие в системе процессы;
- оптимизационные, управляющие процессом, т. е. принимающие те или иные решения;
- многокритериальные, рассматривающие систему по многим критериям;
- игровые, пригодные для исследования и рассматривающие конфликтные ситуации;
- имитационные, максимально использующие имеющуюся информацию о поведении системы.
В качестве примера рассмотрим применение математического моделирования в экологии.
19.4. Математическое моделирование в экологии
Тысячи путей ведут к заблуждению, к истине — только один.
Ж. Ж. Руссо
Для исследования биологических систем, таких как биоценозы, биогеоценозы, можно применять методы математического моделирования и, используя ЭВМ для анализа процессов в этих сложных системах, значительно продвинуть вперед науку о биосфере и экологии.
Например, один из вопросов, который очень часто возникает в современной экологии, состоит в следующем: как определить численность той или иной популяции через определенное время? Ответ на него представляет не только теоретический интерес, но и имеет большое практическое значение. Действительно, не зная этого, нельзя правильно планировать эксплуатацию различных возобновимых природных ресурсов — промысловых рыб, охотничьих угодий и т. п. Для решения этих вопросов можно применить методы математического моделирования.
По распределению и численности видов имеется огромная информация, но ее нужно перевести на математический язык. Естественно, что описание судьбы отдельной особи — задача без-
484
надежная, поэтому вводят макроскопические характеристики, описывающие популяцию. Допустим, в момент времени t0 число особей в популяции в среднем составляет n0. Если п — число особей, то изменение его со временем от числа их рождений g и числа смертей d можно записать в виде:
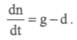
В простейшем случае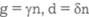 , где коэффициенты , где коэффициенты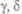
не зависят от общей численности особей. Они могут определяться доступностью пищи, климатом, температурой и т. п. Если эти внешние условия поддерживаются постоянными, то уравнение
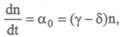
где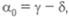 описывает растущую или убывающую по экспо- описывает растущую или убывающую по экспо-
ненте популяцию, т. е. стационарного решения нет, и говорят, что рост не зависит от числа особей. Значит, эти коэффициенты должны зависеть от числа особей. Наиболее важным из всех факторов, которые мы проигнорировали, вероятно, является истощение источников питания, который можно учесть введением в уравнение члена: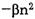 . Тогда получим следующее уравнение: . Тогда получим следующее уравнение:
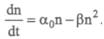
Оно и представляет собой математическую модель процесса изменения численности особей в популяции при котором предполагается, что пища поступает с постоянной скоростью.
Для определения численности особей в популяции в момент времени Т можно воспользоваться математической моделью. Для этого разделим переменные в уравнении и, интегрируя его при условии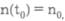 находим следующее уравнение: находим следующее уравнение:
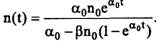
485
Отсюда можно определить число особей в популяции в момент Т:
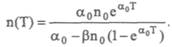
Представим себе, что мы задались целью собирать урожаи с рассматриваемой популяции, т. е. изымать часть особей из экосистемы. Возникает вопрос: когда и сколько собирать урожая, чтобы суммарный урожай за время от t0 до Т был максимален? Это более сложный вопрос, чем предыдущий. Не будем останавливаться на его точном решении, а отметим только, что математическая модель также дает возможность на него ответить. Качественный результат таков: пока число особей в популяции меньше некоторого критического значения, сбор урожая не производится вовсе, в дальнейшем же для достижения максимального суммарного урожая необходимо вести непрерывный сбор его.
Мы рассмотрели весьма упрощенную ситуацию, так как предполагалось, что популяция не взаимодействуют ни с какими другими популяциями, учет же этого обстоятельства, конечно, значительно усложняет модель. При этом могут встретиться ситуации: конкуренция — сосуществование; хищник — жертва; симбиоз. Сосуществование имеет место, когда различные виды не питаются одной и той же пищей, не поедают друг друга, размножаются в разных местах. Тогда уравнения для численности записываются как
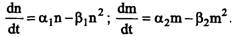
Ситуация усложняется, если виды живут или пытаются жить за счет одного и того же источника пищи или зависят от одних и тех же жизненных условий. Предположим, что обе популяции потребляют один и тот же корм, которого имеется ограниченное количество, и из-за этого находятся в конкурентной борьбе друг с другом. Французский математик В. Вольтерра показал, что при таком предположении динамика популяций
486
достаточно хорошо описывается следующей системой дифференциальных уравнений:
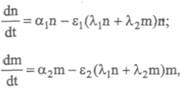
где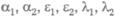 — действительные положительные числа. — действительные положительные числа.
Первые члены правых частей характеризуют скорости роста популяций, если бы не было ограничивающих факторов. Вторые же члены учитывают те изменения в скоростях, которые вызываются ограниченностью корма. Анализ этих уравнений методами теории дифференциальных уравнений позволяет сделать некоторые выводы. Со временем численность одной из популяций становится равной нулю, а численность другой стабилизируется. Та популяция, у которой отношение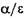 меньше, вымирает, другая же выживает и стабилизируется. меньше, вымирает, другая же выживает и стабилизируется.
В любом биоценозе, кроме отмеченного, происходит взаимодействие между всеми его элементами: особи одного вида взаимодействуют с особями и своего вида, и других видов. Эти взаимодействия могут быть мирными, а могут иметь связь типа "хищник—жертва". Было замечено, что численность хищников колеблется в обратной пропорции относительности колебаний жертв. Анализ этих колебаний позволил Вито Вольтерру вывести необходимые уравнения. Примером анализа таких структур может служить эволюция численности зайцев и волков, которая характеризуется колебаниями во времени. Грубо можно подсчитать, что при их совместном существовании скорость изменения численности зайцев и волков связана с частотой их столкновений, т. е. пропорциональна количеству тех и других с некоторым коэффициентом. Уже эти соображения приведут к системе уравнений, и при определенных условиях система "хищник — жертва" придет в равновесие. В случае неожиданной флуктуации (отстрел волков, гибель зайцев и т. д.) равновесие нарушается, и система приходит в движение. Она ведет себя
487
как колебательная система, когда численность "хищников" и "жертв" начинает колебаться синфазно, с отставанием. Объяснение простое: рост численности зайцев приводит к увеличению питания для волков, но уменьшает количество травы, так что вскоре численность волков вырастает, а зайцев уменьшается. Затем количество травы увеличивается, но запасы пищи для волков уменьшаются, и их численность падает. Тогда поголовье зайцев снова растет, и процесс повторяется. Режим колебаний с определенным периодом оказывается устойчивым.
Модель может усложняться введением нескольких типов жертв, которым может питаться один хищник, и другими вариантами.
Кроме ситуаций "хищник—жертва" и "конкуренция—сосуществование" моделируется ситуация "симбиоз". Модель симбиоза отражает кооперацию отдельных видов в борьбе за существование, когда один вид помогает или покровительствует другому.
В этих рассмотренных нами простых схемах не хватает очень многих факторов: смены климата и погоды, связи возраста особи и смертности, колебаний запасов пищи в разное время года и на разных территориях и т. д. Но использование даже простых моделей при разных, эмпирически учтенных тех или других параметрах дает интересные результаты. Поэтому метод математического моделирования широко применяется не только в современном естествознании, но и во многих гуманитарных науках.
ВЫВОДЫ
- Под системой понимают совокупность компонентов и устойчивых, повторяющихся связей между ними. Разделение систем на простые и сложные является фундаментальным в естествознании. Среди всех сложных систем наибольший интерес представляют системы с так называемой обратной связью.
- Наличие механизма обратной связи позволяет сделать заключение о том, что система преследует какие-то цели, т. е. что ее поведение целесообразно. Наука, которая первой начала
488
исследование подобных систем, получила название кибернетики. Кибернетика — это наука об управлении сложными системами с отрицательной обратной связью.
- Системный подход в науке XX в. — междисциплинарное направление исследований, заключающееся в рассмотрении объекта с точки зрения взаимодействия части и целого. Для системного подхода характерно именно целостное рассмотрение, установление взаимодействия составных частей или элементов совокупности, несводимость свойств целого к свойствам частей.
- Системный подход в корне подрывает прежнее представление о естественно-научной картине мира, когда природа рассматривалась как простая совокупность различных процессов и явлений, а не тесно взаимосвязанных и взаимодействующих систем, различных как по уровню своей организации, так и по сложности. Процесс познания природных и социальных систем может быть успешным только тогда, когда в них части и целое будут изучаться не в противопоставлении, а взаимодействии друг с другом, анализ будет сопровождаться синтезом.
- Выделение биоценозов позволяет использовать методы математического моделирования в экологии. При таком моделировании чаще всего встречаются ситуации: "конкуренция—сосуществование"; "симбиоз"; "хищника—жертва".
- Математическое моделирование различных систем используется в современном естествознании как междисциплинарная методика исследования.
Вопросы для контроля знаний
- Какие системы называются сложными?
- Как понимать обратные связи в системах?
- В чем состоит целесообразность системы?
- Какое значение имеет кибернетика?
- В чем состоит специфика системного исследования?
- Чем отличается система от агрегата?
- Какое различие существует между строением и структурой системы?
489
На чем основано применение математики в системных исследованиях?
- В чем состоят преимущества системного метода исследования?
10. Можно ли применить системный метод к отдельному
предмету?
- Можно ли построить универсальную теорию систем? Обоснуйте ответ.
- Чем отличается системный подход от редукционизма и холизма?
13. Какое мировоззренческое значение имеет системный
метод?
490
.
Комментарии (2)
Обратно в раздел Наука
|
|
