Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Ваш комментарий о книге
Бирюков С., Чередов А. Метрология: Тексты лекций
1. МЕТРОЛОГИЯ. ОСНОВНЫЕ ПОНЯТИЯ В ОБЛАСТИ МЕТРОЛОГИИ
Метрология - это наука об измерениях, о методах и средствах обеспечения их единства и способах достижения требуемой точности [ 2 ].
Метрология зародилась в глубокой древности и по словообразованию означает учение о мерах. В первом русском труде по метрологии (Ф.И.Петрушевский. Общая метрология) приводятся именно ее описательные функции: «Метрология есть описание всякого рода мер по их наименованиям, подразделениям и взаимному отношению». В дальнейшем, в зависимости от усложнения задач, стоящих перед метрологами, происходят изменения в определении понятия «метрология». Так, М.Ф. Маликов приводит уже более широкое, но двоякое определение понятия: «Метрология есть учение об единицах и эталонах» и «Метрология есть учение об измерениях, приводимых к эталонам» [3]. Второе определение свидетельствует о том, что сделан переход от описательных задач непосредственно к измерениям с использованием эталонов. С введением в действие ГОСТ 16263-70 было закреплено определение понятия «Метрология». В этом определении сделан еще больший шаг в сторону практического приложения - обеспечения единства измерений в стране.
Измеряемыми величинами, с которыми имеет дело метрология в настоящее время, являются физические величины, т.е. величины, входящие в уравнения опытных наук (физики, химии и др.). Метрология проникает во все науки и дисциплины, имеющие дело с измерениями, и является для них единой наукой. К основным понятиям, которыми оперирует метрология, можно отнести следующие: физическая величина, единица физической величины, передача размера единицы физической величины, средства измерений физической величины, эталон, образцовое средство измерений, рабочее средство измерений, измерение физической величины, метод измерений, результат измерений, погрешность измерений, метрологическая служба, метрологическое обеспечение и др.
Метрология подразделяется на законодательную метрологию - раздел метрологии, включающий комплексы взаимосвязанных и взаимообусловленных общих правил, требований и норм, а также другие вопросы, нуждающиеся в регламентации и контроле со стороны государства, направленные на обеспечение единства измерений и единообразия средств измерений [2]; теоретическую метрологию – раздел метрологии, посвященный изучению ее теоретических основ; практическую метрологию – раздел метрологии, посвященный изучению вопросов практического применения в различных сферах деятельности результатов теоретических исследований в рамках метрологии и положений законодательной метрологии.
Метрология является научной основой измерительной техники – всех технических средств, с помощью которых выполняется измерение, и техники проведения измерений.
- Основные понятия и определения
Метрология является одной из областей науки и её роль за последние десятилетия чрезвычайно возросла. Метрология проникла и завоевала (или завоевывает) себе позиции во всех областях жизни и деятельности человечества. В силу этого обстоятельства метрологическая терминология тесно соприкасается с терминологией каждой из «специальных сфер».
В нашей стране действует стандарт на терминологию ГОСТ 16263—70 «Государственная система обеспечения единства измерений. Метрология. Термины и определения» и закон об обеспечении единства измерений*, вводящий новые понятия и определения и уточняющий ранее действующие.
Далее в разделе рассматриваются некоторые основные понятия и относящиеся к ним термины и определения, нашедшие широкое применение и выходящее за рамки метрологии. Поэтому их рассмотрение нельзя отнести к какому-либо разделу метрологии. С другой стороны, многие из этих терминов именно в силу их широкого распространения получают искаженное толкование, неправильно применяются или заменяются неправильными терминами. Не установив единства понимания и толкования таких общих терминов, практически невозможно излагать ни одного раздела метрологии.
- Измерение. Измеряемые величины
Определения метрологии и метрологического обеспечения начинаются с основного понятия - измерение. Пожалуй, ни одно определение в области метрологии не вызывает столько споров, как определение этого понятия. Профессором М. Ф. Маликовым было дано следующее определение: «Измерение - познавательный процесс, заключающийся в сравнении путем физического эксперимента данной величины с известной величиной, принятой за единицу сравнения». Недостатком этого определения является то, что оно предполагает сравнение измеряемой величины с ее единицей, что имеет место только при прямых измерениях с использованием метода сравнения с мерой. В частности, это определение не согласуется с косвенными измерениями. К.П.Широковым дано более общее определение: «Измерение - нахождение значения физической величины опытным путем с помощью специальных технических средств». Это определение, включенное в ГОСТ 16263-70, четко определяет границы самого понятия и содержит указания на все важнейшие его элементы. К тому же лаконичность этого определения является его достоинством. Предложения о включении в формулировку определения элементов терминологии кибернетики и теории информации не опровергают стандартизированную формулировку, но усложняют ее понимание и запоминание. Следует отметить, что в нахождение значения физической величины (далее - величины) включается и математическая обработка результатов измерения, в частности введение поправок и статистическая обработка результатов наблюдений (если это требуется).
Значение величины, найденное путем его измерения, называется результатом измерения. Значение величины, полученное при отдельном измерении, называется результатом наблюдения (точнее - измерения). Наблюдением при измерении является экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение из группы значений величины, подлежащих совместной обработке для получения результата измерения.
В определение понятия метрологического обеспечения входит термин «единство измерений», под которым понимается такое состояние измерений, при котором их результаты выражены в узаконенных единицах, размеры которых соответствуют единицам, воспроизводимым эталонами, погрешности результатов измерения известны с заданной вероятностью и не выходят за установленные пределы.
Этот термин позволяет обеспечить сопоставимость измерений, выполненных в разное время, разными средствами и методами. Единство измерений обеспечивается единообразием средств измерений и правильностью методик их выполнения. При этом под единообразием средств измерений понимается такое их состояние, при котором они градуированы в узаконенных единицах и их метрологические свойства соответствуют установленным нормам.
Показателями качества измерений являются погрешность (точность), правильность, сходимость и воспроизводимость измерений.
Погрешность измерения - отклонение результата измерения от истинного значения измеряемой величины.
Точность измерений - их качество, отражающее близость их результатов к истинному значению измеряемой величины.
Правильность измерений - их качество, отражающее близость к нулю систематических погрешностей в их результатах.
Сходимость измерений - их качество, отражающее близость друг к другу результатов измерений, выполняемых в одинаковых условиях.
Воспроизводимость измерений - их качество, отражающее близость друг к другу результатов измерений, выполняемых в различных условиях (в разное время, в различных местах, разными методами и средствами). Ниже будут рассмотрены более подробно все важнейшие элементы, необходимые для осуществления процесса измерений и обеспечения единства измерений [6].
Объектом измерения является физическая величина, характеризующая одно из свойств физического объекта.
Физическая величина, подлежащая измерению, измеряемая или измеренная в соответствии с основной целью измерительной задачи, называется измеряемой физической величиной или просто измеряемой величиной [3].
Измеряемые величины - это величины непосредственно воспринимаемые средствами измерений. Их можно классифицировать с помощью различных признаков, основными из которых являются: природа величины, вид отражаемой стороны эмпирических объектов, метризуемость и изменяемость [8].
По природе измеряемые величины разделяются на 11 классов: электрические, магнитные, электромагнитные, механические, акустические, тепловые, оптические, химические, радиоактивные, пространственные и временные. Каждый класс включает конечное множество конкретных величин.
По виду отражаемой стороны эмпирических объектов каждый класс измеряемых величин разделяется на два подкласса: энергетические и вещественные величины. К энергетическим величинам относятся, например, сила электрического тока, электрическое напряжение, напряженность электрического поля, напряженность магнитного поля, механическая сила, давление и т.п. Метрологическая общность энергетических величин заключается в использовании при их измерении энергии объектов исследования. Вещественными величинами являются различные свойства веществ и материалов, а также параметры физических тел и объектов, например удельное электрическое сопротивление, диэлектрическая проницаемость, магнитная проницаемость, магнитное сопротивление, акустическое сопротивление и т.п. Метрологическая общность вещественных величин состоит в использовании при их измерении измерительных преобразований и других приемов косвенных измерений.
По признаку метризуемости измеряемые величины разделяются на непосредственно и косвенно метризуемые величины. К непосредственно метризуемым величинам относится около двух десятков физических величин, остальные являются косвенно метризуемыми величинами. Непосредственно метризуемые величины измеряются наиболее просто и с высокой точностью. Измерение косвенно метризуемых величин осуществляется с использованием различных функциональных связей и с преобразованием их в непосредственно метризуемые величины.
По признаку изменяемости выделяют состояния и изменения величин. Состояние величины в общем случае характеризуется размером величины, нахождение значения которого и является задачей измерения.
Изменение величины может происходить в пределах какого-либо диапазона размеров и во времени. В зависимости от числа размеров по диапазону различают непрерывные и квантованные по размеру изменения величин. При непрерывном по размеру изменении величины имеется бесконечное число размеров по диапазону. При квантованном по размеру изменении величины в данном диапазоне проявляется конечное число размеров величины.
Изменение величины во времени может быть непрерывным и дискретным (прерывным во времени). При непрерывном изменении величины во времени значения размеров величины определены на данном отрезке времени при бесконечно большом числе моментов времени. При дискретном изменении величины значения размеров величины отличны от нуля только в определенные моменты или интервалы времени. На рис. 1.1 и 1.2 показаны четыре характерные разновидности изменения величин.


Проявления размеров величины по диапазону и во времени могут быть неслучайными (детерминированными) и случайными. Детерминированное изменение величины характеризуется тем, что закон его известен. Случайное изменение величины происходит случайным образом.
Детерминированные непрерывные и дискретные изменения величин подразделяются на периодические и непериодические. Непрерывные периодические и непериодические изменения величин далее подразделяются по виду описывающих их функций. Указанные изменения величин характеризуются обобщенными параметрами и диапазонами их значений.
Для периодически изменяющейся величины x(t) любой формы с периодом Т важными параметрами являются амплитудное xm, среднее
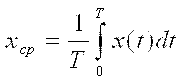 и действующее и действующее  значения, а также значения, а также
частота изменения величин. Непериодическое изменение величины характеризуется максимальным значением, скоростью нарастания и скоростью спада.
Дискретные периодические и непериодические изменения величин подразделяются по форме импульса и характеризуются обобщенными параметрами (мгновенным, амплитудным, средним значениями, а также длительностью импульса, временем нарастания (спада) импульса, частотой следования) и диапазонами их значений.
Случайные непрерывные и дискретные изменения величин разделяются на стационарные и нестационарные. При стационарном изменении величин, в отличие от нестационарного, закон распределения отдельных проявлений размеров не зависит от времени.
Случайные изменения величин описываются различными функциями (функцией распределения вероятностей, функцией плотности распределения вероятностей, автокорреляционной функцией, спектральной плотностью и другими), каждая из которых может определяться вероятностями и количеством реализации, а также диапазонами их значений.
Независимо от того, воспринимается состояние или изменение величины измеряемой величиной, в любом конкретном случае может быть определено мгновенное значение размера величины. При измерении состояния величины, т.е. не изменяющейся во времени величины или весьма медленно меняющейся, процесс измерения может осуществляться в течение длительного времени и к средствам измерения не предъявляется особых требований по быстродействию.
Измерение параметров изменений величин требует повышенного быстродействия средств измерений. При этом помимо мгновенного значения размера величины в качестве измеряемой величины может выступать любой из указанных выше параметров изменений величин.
Различают истинное и действительное значения размера величины. Истинное значение размера величины есть значение размера величины, которое идеальным образом отражает количественную сторону соответствующего свойства объекта. Экспериментально определить его можно только в случае измерения количеств дискретных элементов каких-либо совокупностей, когда погрешность измерения практически может отсутствовать. Получить путем измерения истинное значение размера непрерывного изменения величины невозможно, так как в этом случае погрешности измерения неизбежны. Поэтому на практике часто вместо истинного пользуются действительным значением.
Действительное значение размера величина - это значение, найденное экспериментальным путем и настолько приближающееся к истинному, что может быть использовано вместо него. Определяют его с помощью образцовых средств измерения, погрешностями которых по сравнению с используемыми при измерении средствами можно пренебречь.
* Закон №3, 1994, С. 29-35
- Физическая величина. Единица физической величины
Физическая величина - это свойство, общее в качественном отношении многим объектам (системам, их состояниям и происходящим в них процессам), но в количественном отношении индивидуальное для каждого объекта.
Индивидуальность в количественном отношении следует понимать в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Как правило, термин «величина» применяют в отношении свойств или их характеристик, которые можно оценить количественно, т. е. измерить. Существуют такие свойства и характеристики, которые еще не научились оценивать количественно, но стремятся найти способ их количественной оценки, например запах, вкус и т. п. Пока не научимся их измерять, следует называть их не величинами, а свойствами.
В стандарте есть только термин «физическая величина», а слово «величина» дано как краткая форма основного термина, которую разрешается применять в случаях, исключающих возможность различного толкования. Другими словами, можно называть физическую величину кратко величиной, если и без прилагательного очевидно, что речь идет о физической величине. В дальнейшем тексте настоящей книги краткая форма термина «величина» применяется только в указанном смысле.
В метрологии слову «величина» придано терминологическое значение путем наложения ограничения в виде прилагательного «физическая». Словом «величина» часто пытаются выразить размер данной конкретной физической величины. Говорят: величина давления, величина скорости, величина напряжения. Это неправильно, так как давление, скорость, напряжение в правильном понимании этих слов являются величинами, и говорить о величине величины нельзя. В приведенных выше случаях применение слова «величина» является лишним. Действительно, зачем говорить о большой или малой «величине» давления, когда можно сказать: большое или малое давление и т.п.[4].
Физическая величина отображает свойства объектов, которые можно выражать количественно в принятых единицах. Всякое измерение реализует операцию сравнения однородных свойств физических величин по признаку "больше-меньше". В результате сравнения каждому размеру измеряемой величины приписывается положительное действительное число:
х = q [х] , (1.1)
где q— числовое значение величины или результат сравнения; [х] - единица величины.
Единица физической величины — физическая величина, которой по определению придано значение, равное единице. Можно сказать также, что единица физической величины — такое ее значение, которое принимают за основание для сравнения с ним физических величин того же рода при их количественной оценке.
Уравнение (1.1) является основным уравнением измерения. Числовое значение q находят следующим образом
q = х/ [х] ,
следовательно, оно зависит от принятой единицы измерения [5].
- Системы единиц физических величин
При проведении любых измерений измеряемая величина сравнивается с другой однородной с ней величиной, принятой за единицу. Для построения системы единиц выбирают произвольно несколько физических величин. Они называются основными. Величины, определяемые через основные, называются производными. Совокупность основных и производных величин называется системой физических величин.
В общем виде связь между производной величиной Z и основными может быть представлена следующим уравнением:
Z = LaMbTgIeQhJl,
где L, М, Т, I, Q, J — основные величины; a, b, g, e, h, l— показатели размерности. Эта формула называется формулой размерности. Система величин может состоять как из размерных, так и безразмерных величин. Размерной называется величина, в размерности которой хотя бы одна из основных величин возведена в степень, не равную нулю. Безразмерной называется величина, в размерность которой основные величины входят в степени, равной нулю. Безразмерная величина одной системы величин может быть размерной величиной в другой системе. Система физических величин используется для построения системы единиц физических величин.
Единица физической величины представляет собой значение этой величины, принятое за основание для сравнения с ней значений величин того же рода при их количественной оценке. Ей по определению присвоено числовое значение, равное 1.
Единицы основных и производных величин называются соответственно основными и производными единицами, их совокупность называется системой единиц. Выбор единиц в пределах системы в какой-то мере произволен. Однако в качестве основных единиц выбирают такие, которые, во-первых, могут быть воспроизведены с наивысшей точностью, а во-вторых, удобны в практике измерений или их воспроизведения. Единицы величин, входящих в систему, называются системными. Кроме системных единиц, применяются и внесистемные единицы. Внесистемные единицы — это единицы, не входящие в систему. Они удобны для отдельных областей науки и техники или регионов и поэтому получили широкое распространение. К внесистемным единицам относятся: единица мощности — лошадиная сила, единица энергии - киловатт-час, единицы времени - час, сутки, единица температуры - градус Цельсия и многие другие [9]. Они возникли в процессе развития техники измерений для удовлетворения практических потребностей или введены для удобства пользования ими при измерениях. С теми же целями применяются кратные и дольные единицы величин.
Кратной единицей называется такая, которая в целое число раз больше системной или внесистемной единицы: килогерц, мегаватт. Дольной единицей называется такая, которая в целое число раз меньше системной или внесистемной единицы: миллиампер, микровольт. Строго говоря, многие внесистемные единицы могут рассматриваться как кратные или дольные единицы.
В науке и технике широко распространены также относительные и логарифмические величины и их единицы, которыми характеризуются усиление и ослабление электрических сигналов, коэффициенты модуляции, гармоник и т.д. Относительные величины могут выражаться в безразмерных относительных единицах, в процентах, в промилле. Логарифмическая величина представляет собой логарифм (в радиоэлектронике обычно десятичный) безразмерного отношения двух одноименных величин. Единицей логарифмической величины является бел (Б), определяемый соотношением:
N = lg P1//P2 = 2lg F1/F2 , (1.2)
где P1, P2 - одноименные энергетические величины (значения мощности, энергии, потока плотности мощности и т.п.); F1, F2 - одноименные силовые величины (напряжение, сила тока, напряженность электромагнитного поля и т.п.).
Как правило, применяют дольную единицу от бела, называемую децибелом, равным 0,1 Б. В этом случае в формуле (1.2) после знаков равенства добавляется дополнительный множитель 10. Например, отношение напряжений U1/U2 = 10 соответствует логарифмической единице 20 дБ.
Имеется тенденция к применению естественных систем единиц, основанных на универсальных физических постоянных (константах), которые могли бы быть приняты в качестве основных единиц: скорость света, постоянная Больцмана, постоянная Планка, заряд электрона и т.п. [10]. Преимуществом такой системы является постоянство основания системы и высокая стабильность констант. В некоторых эталонах такие постоянные уже используются: эталон единицы частоты и длины, эталон единицы постоянного напряжения. Но размеры единиц величин, основанных на константах, на современном уровне развития техники неудобны для практических измерений и не обеспечивают необходимой точности получения всех производных единиц. Однако такие достоинства естественной системы единиц, как неразрушаемость, неизменность во времени, независимость от местоположения стимулируют работы по изучению возможности их практического применения.
Впервые совокупность основных и производных единиц, образующих систему, предложил в 1832 г. К. Ф. Гаусс. В качестве основных единиц в этой системе приняты три произвольные единицы—длина, масса и время, соответственно равные миллиметру, миллиграмму и секунде. Позднее были предложены и другие системы единиц физических величин, базирующихся на метрической системе мер и различающихся основными единицами. Но все они, удовлетворяя одних специалистов, вызывали возражения других. Это требовало создания новой системы единиц. В какой-то мере удалось разрешить существовавшие противоречия после принятия в 1960 г. XI Генеральной конференцией по мерам и весам Международной системы единиц, названной сокращенно СИ (SI). В России она вначале была принята как предпочтительная (1961 г.), а затем после введения в действие ГОСТ 8.417—81 «ГСИ. Единицы физических величин» - и как обязательная во всех областях науки, техники, народного хозяйства, а также во всех учебных заведениях.
В качестве основных в Международной системе единиц (СИ) выбраны семь следующих единиц: метр, килограмм, секунда, ампер, Кельвин, кандела, моль.
Международная система единиц включает в себя две дополнительные единицы - для измерения плоского и телесного углов. Эти единицы не могут быть введены в разряд основных, так как они определяются отношением двух величин. В то же время они не являются производными единицами, так как не зависят от выбора основных единиц.
Радиан (рад) - угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу.
Стерадиан (ср) - телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности . сферы площадь, равную площади квадрата со стороной, по длине равной радиусу сферы [7].
В соответствии с Законом об обеспечении единства измерений в Российской Федерации в установленном порядке допускаются к применению единицы величин Международной системы единиц, принятой Генеральной конференцией по мерам и весам, рекомендованные Международной организацией законодательной метрологии.
Наименования, обозначения и правила написания единиц величин, а также правила их применения на территории Российской Федерации устанавливает правительство Российской Федерации, за исключением случаев, предусмотренных актами законодательства Российской Федерации.
Правительством Российской Федерации могут быть допущены к применению наравне с единицами величин Международной системы единиц внесистемные единицы величин.
- Размер величины. Значение величины
Размер физической величины – количественная определенность физической величины, присущая конкретному материальному объекту, системе, явлению или процессу [3].
Иногда возражают против широкого применения слова «размер», утверждая, что оно относится только к длине. Однако заметим, что каждое тело обладает определенной массой, вследствие чего тела можно различать по их массе, т.е. по размеру интересующей нас физической величины (массы). Рассматривая предметы А и В, можно, например, утверждать, что по длине или размеру длины они отличаются друг от друга (например, А > В). Более точная оценка может быть получена лишь после измерений длины этих предметов.
Часто в словосочетании «размер величины» слово «размер» опускают или заменяют его на словосочетание «значение величины».
В машиностроении широко применяют термин «размер», подразумевая под ним значение физической величины - длины, свойственной какой-либо детали. Это значит, что для выражения одного понятия «значение физической величины» применяются два термина («размер» и «значение»), что не может способствовать упорядочению терминологии. Строго говоря, необходимо уточнить понятие «размер» в машиностроении так, чтобы оно не противоречило понятию «размер физической величины», принятому в метрологии. В ГОСТ 16263-70 дано четкое разъяснение по этому вопросу.
Количественная оценка конкретной физической величины, выраженная в виде некоторого числа единиц данной величины, называется «значением физической величины».
Отвлеченное число, входящее в «значение» величины, называется числовым значением.
Между размером и значением величины есть принципиальная разница. Размер величины существует реально, независимо от того, знаем мы его или нет. Выразить размер величины можно при помощи любой из единиц данной величины, другими словами, при помощи числового значения.
Для числового значения характерно, что при применении другой единицы оно изменяется, тогда как физический размер величины остается неизменным.
Если обозначить измеряемую величину через x, единицу величины - через [x1], а отношение их—через q1, то x = q1×[x1] .
Размер величины x не зависит от выбора единицы, чего нельзя сказать о числовом значении q , которое целиком определяется выбором единицы. Если для выражения размера величины x вместо единицы [x1] применить единицу [x2] , то неизменившийся размер x будет выражен другим значением:
x = q2×[x2] , где n2 ¹ n1.
Если в приведенных выражениях применять q = 1, то размеры единиц
x1 = 1×[x1] и x2 = 1×[x2 ] .
Размеры разных единиц одной и той же величины различны. Так, размер килограмма отличается от размера фунта; размер метра—от размера фута и т. п.
1.6. Размерность физических величин
Размерность физических величин— это соотношение между единицами величин, входящих в уравнение, связывающее данную величину с другими величинами, через которые она выражается.
Размерность физической величины обозначается dim A (от лат. dimension – размерность). Допустим, что физическая величина А связана с X, Y уравнением A = F(Х, Y). Тогда величины X, Y, А можно представить в виде
Х = х×[Х]; Y = y×[Y]; A = а×[A],
где А, X, Y - символы, обозначающие физическую величину; а, х, y - числовые значения величин (безразмерные); [A]; [X]; [Y] - соответствующие единицы данных физических величин.
Размерности значений физических величин и их единиц совпадают. Например:
A = X/Y; dim (a) = dim (X/Y) = [Х]/[Y].
Размерность — качественная характеристика физической величины, дающая представление о виде, природе величины, о соотношении ее с другими величинами, единицы которых принимаются за основные.
- Измерительное преобразование
В некоторых случаях, когда нельзя непосредственно сравнить измеряемую величину с воспроизводимой единицей физической величины, используют измерительное преобразование. Это такой вид преобразования, при котором устанавливается однозначное соответствие между значениями двух величин (входной и выходной). Зависимость между этими величинами стремятся сделать линейной. Диапазон преобразования определяется множеством значений входной величины, подвергаемой преобразованию [1].
Вид измерений - часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин. Например, в области электрических и магнитных измерений могут быть выделены как виды измерения электрического сопротивления, электродвижущей силы, электрического напряжения, магнитной индукции и др.
- Методы и средства измерений
Под понятием метод измерения подразумевается совокупность процессов использования принципов и средств измерений.
Принцип измерений - это совокупность физических явлений, на которых основаны измерения. Например, измерение температуры с использованием термоэлектрического эффекта; измерение расхода газа по перепаду давления в сужающем устройстве.
Конкретные методы измерений определяются видом измеряемых величин, их размерами, требуемой точностью результата, быстротой процесса измерения, условиями, при которых проводятся измерения, и рядом других признаков.
Каждую физическую величину можно измерить несколькими методами, которые могут отличаться друг от друга особенностями как технического, так и методического характера. В отношении технических особенностей можно сказать, что существует множество методов измерения и по мере развития науки и техники число их все увеличивается. С методической стороны все методы измерений поддаются систематизации и обобщению по общим характерным признакам. Рассмотрение и изучение этих признаков не только помогает правильному выбору метода и его сопоставлению с другими, но и существенно облегчает разработку новых методов измерения.
Для прямых измерений, при которых искомое значение величины находят непосредственно из опытных данных, можно выделить несколько основных методов: метод непосредственной оценки, дифференциальный метод, нулевой метод, метод совпадений и метод замещений.
При косвенных измерениях, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям, широко применяется измерительное преобразование измеряемой величины в процессе измерений.
Средства измерений - это технические средства, используемые при измерениях и имеющие нормированные метрологические свойства. От средств измерений непосредственно зависит правильное определение значения измеряемой величины в процессе измерения. В число средств измерений входят меры, измерительные приборы, измерительные установки, измерительные системы и измерительные преобразователи; к ним относятся также измерительные принадлежности, которые, однако, не могут применяться самостоятельно, а служат для расширения диапазона измерений, повышения точности измерений, передачи результатов измерений на расстояние и обеспечения техники безопасности в процессе измерения. К средствам измерения не следует относить устройства, служащие для создания заданных условий измерений (различные регулирующие устройства, реостаты, термостаты, барокамеры и т. п.) [4].
Мера - средство измерений, предназначенное для воспроизведения
физической величины заданного размера.
Некоторые меры являются телами определенной формы, изготовленными с необходимой тщательностью. Например, концевые меры длины, гири, измерительные колбы. Другие меры представляют совокупность многих деталей с определенной взаимосвязью (нормальный элемент, измерительный конденсатор, генератор стандартных сигналов), но не это является характерным для мер и их роли в измерениях. Вспомним любой процесс измерения. Относительно редко сравнивают измеряемую величину с мерой, значение которой равно единице. На рычажных весах сравнивают массу взвешиваемого тела с массой гирь 0,1; 0,2; 0,5; 1; 2; 5 кг. Следовательно, любая из этих гирь или их комбинация в процессе измерения может стать исходной для определения измеряемой массы. Таким образом, мера воспроизводит величины, значения которых связаны с принятой единицей этой величины определенным, известным соотношением. Мера - это, как правило, основа измерений [4].
1.11. Эталоны единиц физических величин. Образцовые средства
измерений
Эталон единицы физической величины — средство измерений (или комплекс средств измерений), предназначенное для воспроизведения и хранения единицы данной величины (в некоторых случаях только для воспроизведения или только для хранения единицы). Назначение эталона единицы физической величины - передача ее размера ниже стоящим по точности средствам измерений в общегосударственном или в международном масштабе.
Эталон единицы физической величины выполняется по особой спецификации и официально утверждается в установленном порядке. При конкретном применении термина слова «единицы физической величины» заменяют ее наименованием: эталон килограмма, эталон ампера и т.п. Опускать слова «единицы физической величины» или наименование единицы в целях сокращения следует очень осторожно.
В технике, науке и даже в художественной литературе слово «эталон» употребляется в более широком смысле. Под эталоном понимают образец наивысшего достижения в чем-либо, образец, по которому следует равняться. В метрологии и измерительной технике слово «эталон» следует применять только в том смысле, о котором сказано выше. Неправильно называть наиболее точные средства измерений, применяемые на предприятиях для поверок, эталонами, эталонными средствами измерений. Для них установлены и широко применяются наименования «образцовые средства измерений».
Сам по себе термин «образцовое средство измерений» допускает двоечтение. Он может быть ошибочно понят как лучшее средство измерений и на основании такого толкования может быть применен для измерений в то время, как основное правило метрологии говорит о том, что образцовые меры и образцовые измерительные приборы, предназначенные для поверки, недопустимо применять для измерений, так как это грозит нарушением единства мер и измерений [4].
1.12. Точность измерений
Термин «точность измерения» применяется очень широко, однако пока нет общепринятого способа выражать точность измерения количественно. В ГОСТ 16263—70 сказано: «Количественно точность может быть выражена обратной величиной модуля относительной погрешности. Например, если погрешность измерений равна 10-2 % = 10-4, то точность равна 104. Такой способ количественного выражения точности был предложен давно, однако он широко не распространился.
Под точностью измерения понимают степень приближения результатов измерений к истинному значению измеряемой величины. Однако выражения вроде «точность измерения равна 0,1 %» или «результат измерения верен с точностью до 0,001» неправильны. Термин же «точность» применим лишь для сравнения результатов или относительной характеристики методов измерений, например, точность измерения длины с помощью микрометра больше, чем при измерении с помощью штангенциркуля [4].
1.13. Погрешность измерений
Под погрешностью измерения понимается алгебраическая разность между полученным при измерении значением измеряемой величины и значением, выражающим истинный размер этой величины. Практически мы всегда заменяем значение, соответствующее истинному размеру измеряемой величины (сокращенно истинное значение измеряемой величины), значением, наиболее близким к истинному. По крайней мере, настолько близким, насколько это может удовлетворить нас в каждом данном конкретном случае. Таким образом, результат измерения дает нам только приближенное значение измеряемой величины. И оценить степень этого приближения мы можем тоже только приближенно. Можно ли погрешность измерения назвать ошибкой измерения? Видимо, нет, так как мы не умеем измерять лучше, точнее. Ошибкой измерения можно назвать ошибку, допущенную экспериментатором и обнаруженную при контрольных измерениях. В этих случаях мы говорим, что экспериментатор ошибся.
Выше было сказано, что на практике истинное значение измеряемой величины мы заменяем более близким к нему значением, более точным, чем полученное при измерении. Это значение, более близкое к истинному, мы называем «действительным» значением измеряемой величины.
Действительное значение измеряемой величины - это значение, найденное экспериментальным путем и настолько приближающееся к истинному значению, что для данной цели может быть использовано вместо него. Оно необходимо нам для оценки погрешности измерения, определение которой приобретает теперь несколько другой характер. Погрешность результата измерения - это алгебраическая разность между полученным при измерении и действительным значением измеряемой величины. Это уже реальная величина, доступная для определения.
Погрешность результата измерения может быть выражена в единицах измеряемой величины или в долях (или в процентах) ее значения. Погрешности измерения, выраженные в долях или в процентах от значения измеряемой величины, называют относительными. В отличие от них погрешности, выраженные в единицах измеряемой величины, называют абсолютными [4].
-
Поверка средств измерений
Поверка – совокупность операций, выполняемых органами государственной метрологической службы с целью определения и подтверждения соответствия средства измерений установленным техническим требованиям. Если поверяемые средства измерений предназначены для применения с учетом поправок к их показаниям, то при поверке определяются их погрешности. Если же они предназначены для применения без введения поправок, как, например, используемые в торговле, то при поверке выясняют, не превышают ли их погрешности допускаемые. Кроме того, при поверке производят несколько других операций, чтобы убедиться в отсутствии неисправных или ненадежных узлов, которые могут стать причиной выхода из строя или появления больших погрешностей.
Неправильно поверку средств измерений называть «проверкой», так как слово «проверка» имеет иной смысл. Например, можно проверять выполнение различных требований. Но, с другой стороны, нельзя называть поверкой операции, имеющие целью определение отдельных характеристик или свойств средств измерений. Нельзя говорить «поверка чувствительности», «поверка плоскопараллельности», «поверка исправности». Правильно в этих случаях говорить «определение чувствительности», «проверка плоскопараллельности», «проверка исправности» и т. д. Следует всегда помнить, что поверке могут подвергаться только средства измерений с точки зрения точности.
Сличение средств измерений — разновидность поверки, при выполнении которой проводится сравнение средства измерений того же вида с эталонным или образцовым средством измерений для определения погрешности (меры с мерой, измерительного прибора с измерительным прибором).
Калибровка меры или набора мер - поверка совокупности однозначных мер или одной многозначной меры на различных отметках шкалы, при которой погрешности отдельных мер или значений шкалы оценивают путем сравнения их между собой в различных сочетаниях (отдельные меры, группы мер или отдельные участки шкалы).
Согласно Закону об единстве измерений стандарту калибровка - это совокупность операций, выполняемых с целью определения и подтверждения действительных значений метрологических характеристик и (или) пригодности к применению средства измерений, не подлежащего метрологическому контролю и надзору.
Иногда термин «калибровка» употребляют как синоним поверки, однако это неправильно, так как калибровкой можно называть лишь такую поверку, при которой сравниваются несколько мер или деления шкалы между собой в различных сочетаниях.
Градуировка средств измерений - нанесение отметок на шкалу или определение значений измеряемой величины, соответствующих уже нанесенным условным отметкам. При отсутствии шкалы под градуировкой понимают определение зависимости между измеряемой и другой величиной, легко определяемой по показаниям измерительного прибора, например, зависимости значений световых величин, воспроизводимых светоизмерительной лампой, от силы тока, протекающего по ее нити и т. п. Во всех этих случаях речь идет об определении градуировочной характеристики средств измерений. Поэтому более кратко градуировка средства измерения—это определение градуировочной характеристики средства измерения. В технической литературе можно встретить неправильное употребление этих терминов, когда поверку называют градуировкой, градуировку — калибровкой и т.п. Иногда эти термины заменяют другими, неверными и не отражающими существа метрологической операции, например, «тарировка» вместо «поверка» или «градуировка» [4].
.
Ваш комментарий о книге
Обратно в раздел Наука
|
|
