Библиотека Гумер - Экономика и менеджмент

Приложение 1. Примеры и задачи

ОГЛАВЛЕНИЕ

1.1. Дисконтирование денежных поступлений одного года

Дисконтирование — это приведение разновременных показателей к какому-либо одному моменту времени — точке приведения.
Существует несколько методов дисконтирования. Все они основаны на допущении, что деньги, которые должны быть получены (или израсходованы) в будущем, будут иметь меньшую ценность, чем в текущий момент.
Предположим, что у нас скопилась некоторая сумма денег, которую мы решили поместить в банк. Нам предлагают, к примеру, вместо 240 тыс. руб., вложенных сегодня, через год вернуть 300 тыс. руб. Иначе говоря, 300 тыс. через год и 240 тыс. сейчас для нас эквивалентны:

Коэффициент А — это пропорция между инвестируемой в текущий момент суммой и той суммой, которую нам через год предстоит получить в банке. В рассматриваемом случае:

Как мы видим, коэффициент А < 1 уменьшает (дисконтирует) ожидаемую в будущем сумму до размеров той суммы, от которой мы отказываемся в настоящем. Коэффициент А принято называть коэффициентом дисконтирования, а процесс вычисления суммы, от которой нужно отказаться сейчас ради получения известной суммы в будущем, именуется дисконтированием. Коэффициент дисконтирования всегда меньше 1, поскольку в ином случае деньги сегодня стоили бы много меньше чем завтра. В общем виде:

где PV — стоимость будущих поступлений в настоящее время, или текущая стоимость (англ. presentvalue); С1 — поступления будущего года (англ. cashflow). Из формулы (П.1.1) следует:

Это выражение позволяет определить текущую стоимость будущих поступлений. Разница между поступающей в будущем и дисконтированной к настоящему времени стоимостью составляет доход. В нашем примере он равен 60 тыс. руб.
Если соотнести между собой доход, получаемый через год, с размером средств, которые необходимо инвестировать в настоящее время, то можно определить доходность (ставку доходности) такой операции:

Отсюда можно заключить:

где Е — ставка доходности.
В результате некоторых преобразований формулы (П. 1.3) получаем:

или

Тогда

откуда

Здесь t — номер шага расчета, t = 0, 1, 2, 3,..., Т, где Т — горизонт расчета. Если же норма доходности (дисконта) меняется во времени и на t-мшаге расчета достигает Et, то А0 = 1 и Аt = 1/РV( 1 + E) при t > 0.
Таким образом, коэффициент дисконтирования зависит от того (обратно пропорционален тому), какой годовой доходности ожидает инвестор от вложения своих сбережений.
Для закрепления полученных знаний предлагаем решить следующие задачи.
Задача 1. Определите доходность ваших вложений, если вы вложили 150 (200, 400, 600) тыс. руб., а через год получили соответственно 200 (300, 600, 900) тыс. руб. Оцените какую сумму выгоднее вкладывать.
Задача 2. Определите, каковы должны быть поступления через год, если при ставке доходности 10 (20, 30, 40, 50, 60, 70, 80, 90, 100) % годовых вы вложили соответственно 200 (300, 400, 500, 600, 700, 800, 900, 1000, 1100) тыс. руб.
Задача 3. Определите, какова должна быть текущая стоимость будущих поступлений, чтобы через год при ставке доходности 10 (20,30,40,50, 60, 70, 80, 90, 100) % годовых получить соответственно 100 (300, 400, 500, 600, 700, 800, 900, 1000, 1200) тыс. руб.
Задача 4. Определите доходность на основании условий задач 2 и 3 при С1 = 1000 (10000, 12000, 12000, 14000, 15 000) и PV = 800 (7000, 8000,9000, 7000, 8000),

1.2. Дисконтирование денежных поступлений разных лет

Известно, что любое отчуждение денежных средств приносит инвестору неудобства, обусловленные отказом от возможности лучшего вложения средств. Поэтому инвестор вряд ли согласится вкладывать средства более чем на год по ставке доходности, принятой при вложениях на год. Он потребует компенсации за все дополнительные неудобства. Эта компенсация может состоять не только в повышении ставки доходности, но и в сокращении объема вложения денежных средств в начальном периоде. По-видимому, такую компенсацию инвестор получит, вкладывая меньшую сумму, чем та, которая была бы помещена сроком на один год.
Обозначим поступления второго года (начиная отсчет с текущего момента) через С2, коэффициент дисконтирования этой суммы — через А2, а искомый объем инвестиций — через PV2. Тогда: PV = А2 •С2.
Предположим, что мы собираемся получить от данной операции доход 25 % годовых за каждый из предстоящих до выплаты двух лет.
Задача решается поэтапно. Поступающая через два года сумма в 125 тыс. руб. будет «стоить» за год до этого (т. е. через год от настоящего момента):

Это значит, что на следующий год следовало бы инвестировать 100 тыс. руб. для того, чтобы спустя год после этого (т. е. через два года от настоящего момента) получить 125 тыс. руб. Возникает вопрос: какую сумму надо инвестировать сейчас, чтобы на следующий год получить эти 100 тыс. руб., которые будут инвестированы для получения 125 тыс. руб. через два года?
Ответ таков:

Обобщая сказанное, запишем:

В рассматриваемом примере:

Коэффициент дисконтирования равен:

В более общем виде  (для любого числа лет между датой инвестирования и датой выплаты причитающейся суммы) формула выглядит так:

где п — число лет между датой инвестирования и датой выплаты причитающейся суммы; Сп - сумма, причитающаяся к выплате через п лет; Еп —доходность инвестирования в течение п лет; PVn - современная дисконтированная стоимость денежной суммы, учитывающая все неудобства в течение п лет; Аn—коэффициент дисконтирования денежных поступлений, приходящийся на n-й год.
Коэффициент дисконтирования сумм n-го года равен при этом:

Для закрепления материала решите нижеследующие задачи.
Задача 1. Сколько денег надо инвестировать сейчас, чтобы через 3 (5, 8, 10) лет получить соответственно при доходности 30 (40, 50, 60) % годовых 3 (6, 7, 8) млн руб.?
Задача 2. Сколько денег получит вкладчик по истечении 3 (5, 8, 10) лет, если он сегодня вложил соответственно под 60 (70,80,90) % годовых 1 (2,3, 4) млн руб.?
Задача 3. Определите фактическую и ожидаемую доходность от инвестирования одной и той же суммы на разные сроки (см. условие задачи 2), если банк уменьшил ставку доходности на 20 %. (Здесь необходимо отметить, что ожидание той или иной доходности в первую очередь может быть обусловлено темпами инфляции, политикой Центробанка, спросом на деньги.)

1.3. Расчет текущей стоимости с многоразовых поступлений от инвестиций

Представим себе следующую ситуацию: имеется некий инвестиционный проект, который требует в первый период времени (год) вложения 125 млн руб., во второй — 150 млн руб., в третий — 160 млн руб. При этом ставки доходности соответственно составляют 25,30 и 40 % годовых. Какую сумму можно инвестировать сейчас в указанный инвестиционный проект?
Задача решается по частям, исходя из требований инвестирования и с учетом ставок доходности:

Сложив эти три значения, получим сумму, которую нужно вложить сейчас:

В обобщенном виде формула выглядит так:

где t—номер года, t = 1,..., n; Ct—- поступления t-гo года; Et — доходность t-гогода. Для закрепления материала предлагаем на основе условий, представленных в табл.П. 1.1. определить сумму вложений в проекты в настоящее время.

Таблица П. 1.1

Представьте себе, что вы ограничены в средствах, а потому вынуждены при прочих равных условиях выбирать такой проект, который в настоящее время требует вложить меньше всего средств. Исходя из данных табл. П. 1.1., выявите лучший проект.
Для каждого инвестиционного проекта, предполагающего многоразовые поступления в течение нескольких лет, можно определить структуру ставок доходности.
При этом инвесторы всегда ориентируются на среднерыночные ставки доходности, под которыми понимают уровни доходности от вложений в предприятия определенных отраслей или же процентные ставки для средне- и долгосрочных банковских кредитов. Вот почему такую структуру доходности иногда называют повременной структурой процентных ставок (англ. term structure of interest rates).
Общая структура ставок доходности помогает сопоставить инвестиционные альтернативы. Предположим, есть 7000 млн руб., которые необходимо израсходовать на выполнение некоторого инвестиционного проекта предприятия. Ряд организаций предлагают свои услуги в проектировании и осуществлении инвестиционных проектов. Поскольку все проекты имеют одинаковую направленность и различаются лишь незначительными особенностями, нам нужно выбрать наиболее приемлемый для инвестирования проект, допустив, что степень риска и прочие условия одинаковы.
Исходные данные приведены в табл. П.1.2.

Таблица П. 1.2

Для поиска наилучшего решения используем формулу (П.1.9):
Тогда:

Результаты вычислений свидетельствуют, что при использовании средних рыночных ставкок в проект А следует инвестировать не более 6684,4 млн руб., в проект Б — не более 8162,5 млн руб., в проект В — не более 6416 млн руб., в проект Г — не более 8622,3 млн руб. Если мы вложим в каждый из проектов по 7000 млн руб., то проект А принесет убыток 315,6 млн руб.; проект Б даст экономию 1162,5 млн руб., проект В нанесет ущерб в размере 584 млн руб., проект Г сэкономит 1622,3 млн руб. Следовательно, проекты Б и Г предлагают инвестиционные решения, которые выгоднее рыночных, а проекты А и В — хуже рыночных.
Основываясь на изложенных выше посылках, оцените выгодность вариантов вложения 8000 млн руб. в проекты, характеризуемые данными табл. П.1.3—П.1.5.

Таблица П. 1.3

Таблица П. 1.4

Таблица П. 1.5

На практике при анализе различных типов инвестиций приходится рассматривать многократные поступления, связанные с поэтапной оплатой работ (проектно-исследовательских и опытно-конструкторских работ, установки оборудования и др.).
В этом случае порой возникают затруднения с определением текущей цены инвестиционного проекта. Как правило, задачи подобного типа решаются путем приведения инвестиций, осуществляемых в будущих периодах, к настоящему моменту времени, исходя из ставки доходности за тот год, в котором они производятся.
Например, имеется некий инвестиционный проект, требующий первоначального взноса в размере 100 млн руб. и повторного (через год) в размере 200 млн руб. Лишь затем последуют поступления: через два года 300 млн руб., а на третий — 100 млн руб. Выгоден ли проект, если структура доходности такова: 1-й год — 10%, 2-й - 15 %, 3-й - 20 %?
Рассмотрим дисконтированную стоимость проекта. По сути, мы определяем стоимость инвестиций, которые необходимо осуществить сегодня, вместо того чтобы вкладывать средства в соответствующем году. Решение задачи сводится к нахождению

Это значит, что инвестируемые в соответствующие годы 300 млн руб. «стоят» сейчас только 281,8 млн руб. При этом первоначальный взнос тоже как бы дисконтируется, но с коэффициентом, равным 1.
Определим уже известным способом текущую стоимость будущих поступлений (доход) от реализации проекта:

Следовательно, для реализации проекта необходимо сейчас вложить 281,8 млн руб. и получить 284,7 млн руб. Отсюда разница между текущей дисконтированной стоимостью и необходимыми для его реализации вложениями составляет

Итак, мы получим чистую текущую стоимость проекта, которая определяется путем вычета суммы первоначальных инвестиций в проект из текущей стоимости проекта. Исчисленное значение больше нуля, значит, данный проект более выгоден, чем инвестиции на среднерыночных условиях. Если бы значение ЧТС оказалось меньше нуля, то он был бы менее выгодным.
Для закрепления полученных знаний предлагаем решить ряд задач по оценке эффективности вложений, условия которых приведены в табл. П.1.6-П.1.9.

Таблица П. 1.6

Таблица П. 1.7

ТаблицаП. 1.8

Таблица П. 1.9

1.4. Определение текущей стоимости «вечных» проектов

Несколько слов о «вечных» проектах. Как правило, так именуют инвестиции, которые не предполагают возврата вложенных сумм, но дают возможность периодически получать деньги на протяжении всего «срока жизни» проекта, т. е. фактически вечно.
В качестве подобных инвестиционных проектов правомерно рассматривать вложения в простые акции акционерных обществ, по которым нельзя потребовать возврата денежных сумм от эмитента, а можно лишь получать ежегодные дивиденды и довольствоваться приростом рыночных цен на эти акции. Однако еще более полно черты «вечного» инвестиционного проекта воплощают в себе привилегированные акции с фиксированным ежемесячной процентной ставкой.
Поскольку на практике сложно выстроить в ряд и рассчитать бесконечно большое число текущих стоимостей каждого предстоящего в будущем поступления, используются некоторые допущения, а именно:

• все ежегодные выплаты по «вечному» инвестиционному проекту равны между собой и составляют одну и ту же сумму в каждом из будущих годов (т. е. С1 = С2 = ... = Сп = const);
• ставка доходности для всех будущих лет одинакова (т. е. Е1 = Е2 = ... = Еп = const).

Допущения позволяют упростить процедуру дисконтирования и рассчитывать текущую стоимость всех будущих поступлений от «вечного» инвестиционного проекта по формуле:

где С — объем денежных поступлений каждого года (периода); Е — доходность для каждого года (периода).
Например, вам предлагают инвестировать средства в акции АО «Русские самоцветы», которое собирается всю полученную им прибыль ежегодно раздавать инвесторам в виде дивидендов. Предполагается также, что объем дивидендов не будет изменяться из года в год и составит 20 тыс. руб. на каждую акцию. Сколько должна стоить одна акция, чтобы от ее покупки вы получили 40 % годовых? Решить эту задачу помогает формула (П.1.10).
При С = 20 000 руб., Е = 40 % = 0,4

Это значит, что за акцию необходимо заплатить 50 тыс. руб. Если же вы купите акцию по меньшей цене, то вложение окажется выгоднее среднерыночного, т. е. вы выиграете, если заплатите больше — проиграете. Наконец, в случае приобретения акции за 50 тыс. руб. акции принесут ожидаемый среднерыночный доход в размере 40 % годовых.
Однако каждое акционерное общество обещает акционерам каждый год увеличивать объем дивидендных платежей. При этом темп ежегодного прироста дивидендов не меняется, т. е. дивиденд каждого последующего года увеличивается на одно и то же число процентов rfo сравнению с дивидендным платежом предыдущего года. Например, дивиденд первого года равен 20 тыс. руб., второго — 24 тыс. руб., третьего — 28,8 тыс. руб. и т. д., с каждым годом он увеличивается на 20 % по сравнению с предыдущим годом.
Определим, какова должна быть текущая стоимость «вечного» инвестиционного проекта с возрастающими платежами, чтобы обеспечивать доход в размере 40 % годовых. Ряд нарастающих дивидендных платежей выглядит следующим образом:
С1 = 20 тыс. руб.
С2 = - C1• l,2 = C1(1+  q) = 24 тыс. руб.
С3 = С2 • 1,2 = С1 • 1,2 • 1,2 = С1 (1 + q)2 = 28,8 тыс. руб.;
С4= С3 • 1,2 = С1 (1 + q)3 = 34,56 тыс. руб.,
где q= 20 % = 0,2 — ежегодный прирост процентного платежа;
Рассчитаем текущую стоимость будущих поступлений:

PV1= С1 / (1 + E) = 20/1,4 = 14,286 тыс. руб.;
PV2 = С2 / (1 + Е)2 = С1 (1 + q) / (1 + E)2 = 24 / 1,42 = 12,245 тыс. руб.;
PV3 = С3 / (1 + E)3 = С1 (1 + q)2 / (1 + E)3 = 28,8 / 2,74 = 10,511 тыс. руб.;
PV4 = С4 / (1 + E)4 = С1 (1 + q)3 / (1 + E)4 = 34,56 / 3,84 = 9 тыс. руб.

Сумма текущих стоимостей всех будущих поступлений составит:

Рассчитать стоимость указанным способом для любого «вечного» проекта невозможно. Поэтому формулу для расчета упрощают и приводят к виду:

где Сi — сумма платежа первого (следующего года,); E — ставка среднесрочной доходности; q— темп ежегодного прироста процентного платежа.
При С1 = 20 тыс. руб., Е = 0,4, q = 0,2:

Значит, ежегодный прирост дивидендных платежей на 20 % по сравнению с первоначальным периодом значительно увеличится в будущем.
Для закрепления полученных знаний предлагаем решить нижеследующие задачи.
Задача 1. Рассчитайте стоимость акции при С= 30, (40, 45, 50, 60, 70, 80) тыс. руб. и Е= 10 (20, 15, 20, 30, 35, 40) %.
Задача 2. Определить текущую стоимость всех будущих поступлений, исходя из следующих данных:

2. Основные принципы оценки эффективности инвестиционных проектов

Эффективность инвестиционных проектов и отдельных мероприятий оценивают, чтобы определить целесообразность вложений. Для этого информация, полученная в ходе проектного анализа, анализируется с использованием ряда процедур и правил, которые помогают лицу, принимающему решение, сделать вывод о выгодности инвестирования с точки зрения максимизации доходов и минимизации риска.
Следует особо подчеркнуть, что инвестиционный проект можно рассматривать как изолированный, если он сформирован под выбранную идею, которая не исключает возможности совершенствования. В любом случае речь идет об одном направлении инвестирования, исключает возможность рассмотрения других вариантов инвестирования в различные направления развития фирмы, несмотря на их возможную привлекательность.
Если же фирма стоит перед проблемой выбора стратегии развития и максимизации дохода, то необходимо рассмотреть альтернативные проекты, намечающие разные пути достижения одной цели в рамках заданного отрезка времени. К примеру, доход можно увеличить как за счет обновления технологического оборудования, так и за счет совершенствования организации и технологии производства существующего ассортимента. Иными словами, фирма должна сначала выбрать направление инвестирования и лишь затем рассматривать эффективность того или иного инвестиционного проекта.
Не следует забывать и о другом: все затраты и результаты, связанные с осуществлением проектов, носят денежный характер.
Таким образом, проект считается эффективным, если отвечает следующим условиям:
чистая прибыль от инвестирования превышает прибыль от вложений на банковский депозит;
ставка доходности инвестиций выше уровня доходности;
эффективность проекта с учетом фактора времени выше эффективности альтернативных проектов;
рентабельность активов предприятия после осуществления проекта увеличивается и как минимум превышает среднюю процентную ставку банковского кредита; проект основан на маркетинговых исследованиях, намечающих линию поведения предприятия на рынке товаров и услуг с учетом потенциальной емкости рынка и его основных сегментов, платежеспособного спроса, объемов реализации продукции;
учтены экологические аспекты, в том числе выполнены прогноз и стоимостная оценка природоохранных мероприятий;
приняты во внимание социальные последствия реализации проекта, а именно: изменение количества рабочих мест в административно-территориальном образовании, изменение условий труда работников, улучшение жилищных и культурно-бытовых условийработников, изменение структуры производственного персонала и др.
В качестве ключевых показателей рассматривают финансовую состоятельность и экономическую эффективность проекта.
Финансовая состоятельность, или коммерческая оценка, характеризует платежеспособность проекта, приток П(t) и отток O(t) денежных средств (англ. cash flow).
Исходными данными для оценки экономической эффективности служат произведенные или планируемые денежные поступления и выплаты.
Приток денежных средств формируется за счет доходов от реализации продукции (услуг), внереализационных доходов, поступлений от эмиссии акций и привлечения средств на возвратной основе и др.
Отток определяется инвестиционными издержками, текущими затратами, платежами в бюджет, обслуживанием внешней задолженности (выплатой процентов и погашением займов) и др.
Таким образом, для оценки эффективности проектов используется система показателей, отражающих соотношение затрат и результатов применительно к интересам его участников.
Согласно «Методическим рекомендациям по оценке эффективности инвестиционных проектов» различают показатели:
коммерческой (финансовой) эффективности, учитывающие финансовые последствия реализации проекта для его непосредственных участников;
бюджетной эффективности, отображающие финансовые последствия осуществления проекта для федерального, регионального или местного бюджетов;
экономической эффективности, учитывающие затраты и результаты, которые связаны с реализацией проекта, выходят за пределы прямых финансовых интересов участников инвестиционного проекта и допускают стоимостное измерение. Для крупномасштабных (существенно затрагивающих интересы города, региона или всей России) проектов рекомендуется обязательно оценивать экономическую эффективность.
Предстоящие затраты и результаты при определении эффективности инвестиционного проекта оценивают в пределах расчетного периода, продолжительность которого (горизонт расчета) принимают с учетом:
продолжительности создания, эксплуатации и, при необходимости, ликвидации объекта;
средневзвешенного нормативного срока службы основного технологического оборудования;
достижения заданных характеристик прибыли (массы и/или нормы прибыли и т. д.);
требований инвестора.
Горизонт расчета измеряется числом шагов расчета, которые при определении показателей эффективности в пределах расчетного периода могут составлять месяц, квартал или год.
Затраты участников подразделяются на первоначальные (единовременные, капиталообразующие), осуществляемые на стадии строительства, текущие, относящиеся к стадии функционирования, и ликвидационные, которые сопряжены с ликвидацией.
Капиталообразующие затраты определяют как сумму средств, необходимых для строительства (расширения, реконструкции, модернизации) и оснащения оборудованием инвестируемых объектов, расходов на подготовку капитального строительства и прироста оборотных средств, необходимых для нормального функционирования предприятий. Укрупненно эти затраты складываются из следующих статей:
приобретения или аренды земли;
подготовки строительной площадки;
проектно-конструкторских работ;
предэксплуатационных капитальных работ;
приобретения машин и оборудования;
строительства зданий и инженерных сооружений; увеличения оборотного капитала;
непредвиденных расходов.
Для стоимостной оценки результатов и затрат используют базисные, мировые, прогнозные и расчетные цены.
Под базисными ценами (Цб) понимают такие, которые сложились в экономике страны на определенный момент времени tб. Базисная цена на любую продукцию или ресурсы считается неизменной в течение всего расчетного периода. Измерять экономическую эффективность в базисных ценах следует на стадии технико-экономических исследований инвестиционных возможностей.
Прогнозную цену Ц(t) продукции или ресурса в конце t-гoшага расчета (например, t-гогода) находят по формуле:

где Цб — базисная цена продукции или ресурса; J(t, tн) — коэффициент (индекс) изменения цен продукции или ресурсов соответствующей группы в конце t-гoшага по отношению к начальному моменту расчета (в который известны цены).
Для проектов, осуществляемых по заказу органов государственного управления, значения индексов изменения цен на отдельные виды продукции или ресурсов следует устанавливать в задании на проектирование в соответствии с прогнозами Минэкономики РФ.
Расчетные цены применяют для вычисления интегральных показателей эффективности, если текущие значения затрат и результатов выражены в прогнозных ценах. Это необходимо, чтобы обеспечить сравнимость результатов, полученных при различных уровнях инфляции.
Расчетные цены получаются путем введения дефлирующего множителя, соответствующего индексу общей инфляции.
Сравнение различных инвестиционных проектов (или вариантов проекта) и выбор лучшего из них рекомендуется производить с использованием различных показателей, к которым относятся:
чистый дисконтированный доход (ЧДД), илиинтегральный эффект Эинт[взарубежной терминологии — чистая приведенная стоимость NPV(от англ. netpresentvalue)];
индекс доходности (ИД) [индекс прибыльности PI(от англ. profitabilityindex)];
внутренняя норма доходности (ВИД) [внутренняя норма прибыли, рентабельности, возврата инвестиций IRR(от англ. internalrateofreturn)];
срок окупаемости;
другие показатели, отражающие интересы участников или специфику проекта.
Показатели, используемые для сравнения различных инвестиционных проектов (вариантов проекта), должны быть приведены к сопоставимому виду.
Чистый дисконтированный доход рассчитывают как сумму текущих эффектов за весь расчетный период, приведенную к начальному шагу, или как разницу между интегральными результатами и интегральными затратами.
Если в течение расчетного периода не происходит инфляционного изменения цен или расчет производится в базовых ценах, то значение ЧДД для постоянной нормы дисконта вычисляют по формуле:

где Rt — результаты, достигаемые на t-мшаге расчета; Зt — затраты, осуществляемые на t-мже шаге; Т — горизонт расчета, равный номеру шага, на котором объект ликвидируют.
Следует особо подчеркнуть, что в данной и последующих формулах в конце t-гo(последнего) шага должна учитываться реализация активов (условная). Если же предусматривается действительная ликвидация производства, она должна найти отражение в проекте. Чистую ликвидационную (остаточную) стоимость объекта получают вычитанием расходов на ликвидацию из выручки от реализации материальных ценностей, полученной при ликвидации.
Если ЧДД инвестиционного проекта положителен, проект является эффективным (при данной норме дисконта). Чем больше ЧДД, тем эффективнее проект. Осуществление инвестиционного проекта при отрицательном ЧДД угрожает инвестору убытками, т. е. проект неэффективен.
На практике формулу ЧДД часто модифицируют, исключая из состава Зtкапитальные вложения и обозначая через Kt — капиталовложения на t-м шаге, К — дисконтированные капиталовложения:

Положительное значение К указывает на уоыток, отрицательное — на доход.
Обозначив как Зt* — затраты на t-мшаге, не включающие капиталовложения, запишем:

Эта формула выражает разницу между суммой приведенных эффектов и приведенными к тому же моменту времени капитальными вложениями К.
Индекс доходности ИД представляет собой отношение суммы приведенных эффектов к капиталовложениям:

Индекс доходности тесно связан с ЧДД. Он строится из тех же элементов, его значение зависит от значения ЧДД: если ЧДД > 0, то ИД > 1, если ЧДД < 0, то ИД < 1. При ИД > 1 проект эффективен, при ИД < 1 — неэффективен.
Внутренняя норма доходности ВНД есть норма дисконта Евн, при которой сумма приведенных эффектов равна приведенным капиталовложенным. Другими словами, Евн (ВНД) является решением уравнения:

При определении ВНД надо соблюдать известную осторожность, поскольку внутренняя норма доходности в ряде случаев не всегда существует или же имеет несколько значений, вследствие чего корректный расчет ее несколько затруднен.

Формально ВНД исчисляют как то значение коэффициента дисконтирования, при котором ЧДД = 0, т. е. инвестиционный проект не обеспечивает роста доходности предприятия, но и не ведет к ее снижению. Именно поэтому в отечественной литературе ВНД иногда называют поверочным дисконтом. Она позволяет найти граничное значение коэффициента дисконтирования, разделяющее инвестиции на приемлемые и невыгодные. Для этого ВНД сопоставляют с тем уровнем окупаемости, который предприятие (инвестор) выбирает для себя в качестве стандартного с учетом того, по какой цене само оно получило капитал и какого уровня «чистой» прибыли хотело бы достигнуть. Этот стандартный уровень желаемой рентабельности вложений часто называют барьерным коэффициентом HR(от англ. herdlerate). Принцип использования названных показателей таков: при ВНД > НR — проект приемлем, при ВНД < HR — неприемлем, при ВНД = HRможно принимать любое решение.
Кроме того, ВНД служит своего рода «ситом», помогающим отбраковывать невыгодные проекты по ставкам доходности, а также индикатором уровня риска: чем большее ВНД превышает принятое предприятием значение HR, тем больше запас прочности проекта и тем меньше угрозы несут в себе возможные ошибки при оценке объема будущих денежных поступлений.
Для стандартных инвестиций справедливо следующее утверждение: чем выше коэффициент дисконтирования, тем меньше ЧДД (рис.П. 1.1).

Как видно из рис.П.1.1, ВНД — это то значение коэффициента дисконтирования Е, при котором кривая зависимости ЧДД от Е пересекает горизонтальную ось, т. е. ЧДД оказывается равным нулю. Найти ВНД можно двумя способами: во-первых, рассчитать с помощью уравнения (П.1.17), а во-вторых, отыскать в таблицах коэффициентов приведения.
Практически всегда осуществление инвестиционного проекта сопряжено с риском, т. е. вероятностью неполучения инвестором требуемой прибыли от реализации проекта вследствие неблагоприятных событий.
Известно, что риск зависит от множества факторов, влияние которых не всегда поддается учету. Поэтому на практике учет состоит в выборе такой нормы дисконтирования будущих поступлений, которая соответствовала бы складывающейся ситуации. Поскольку при оценке инвестиционных проектов во многих случаях отсутствует точная информация о возможных результатах и затратах, то необходимо опираться на прогнозы. Эти прогнозы устанавливают вероятность того, что определенный эффект Эt = Rt - Зt будет иметь место в анализируемом периоде t, где Rt — результаты от реализации товаров или услуг, а Зt — затраты.
Если, например, в t-м временнум интервале некоторое значение эффекта Эtj (j = 1,n) может иметь место с вероятностью pj (j= 1, п), тогда можно найти математическое ожидание в этом временном интервале по формуле:

где Эt— ожидаемый эффект (математическое ожидание эффекта).
С учетом того, что Эt= рt -Зt, формула (П. 1.18) может быть преобразована к виду:

т. е. ожидаемый эффект Эt равен разности ожидаемых результатов Rtи затрат Зt.
Найденное по выражениям (П.1.18) или (П.1.19) значение ожидаемого эффекта подставляют в приведенную выше формулу ЧДД вместо однозначно детерминированной оценки дохода:

Соответственно Rt - Зtнеобходимо рассматривать как эффект, который в зависимости от риска может колебаться в определенном интервале. Вместе с тем отклонение от математического ожидания (при большом числе наблюдений его можно считать средней величиной) является среднеквадратическим отклонением о, причем чем больше среднеквадратическое отклонение, тем выше риск. Среднеквадратическое отклонение σ для эффекта Эt определяют по формуле:

Следует особо подчеркнуть, что выражение (П.1.21) справедливо в том случае, если результаты реализации продукции и затраты на ее производство взаимозависимы и изменяются согласованно, к примеру в соответствии с объемом продаж продукции. Но, как показывает практика, затраты и результаты могут изменяться независимо, тогда:

Общий риск по инвестиционному проекту рассчитывают как среднеквадратическое отклонение интегрального экономического эффекта (ЧДД).
Если для среднеквадратического отклонения справедливо выражение (П. 1.21), (ЧДД) находят по формуле:

Если же результаты Rt и затрат Зt — независимые переменные и справедливо выражение (П. 1.22), то среднеквадратическое отклонение для интегрального экономического эффекта определяют по формуле:

Во многих случаях удобнее пользоваться не среднеквадратическим отклонением, а относительным риском, определяемым как отношение квадратического отклонения к ожидаемому значению:

При высокой степени риска инвестор может решиться на дисконтирование, если предполагаемый доход будет достаточно высоким. Существует определенная зависимость между риском и размером необходимых доходов. Эта зависимость может быть представлена кривой безразличия, показывающей связь между σ и необходимой прибылью П(σ), измеряемой в процентах. При отсутствии риска (σ = 0) норма дисконтирования равна Е0,а соответствующая прибыль — П0. Если риск равен σ*, то для того чтобы инвестор решился дисконтировать проект, прибыль должна быть не меньше П*, т. е. рисковая премия должна составлять не менее П* - П0.Соответственно норма дисконта увеличивается до R* большего R0. Приведенную на рис. П. 1.2 кривую можно отнести к кривой безразличия, так как для инвестора равноценны все проекты, соответствующие точкам этой кривой, а определенный риск компенсируется соответствующим приростом прибыли.

Для закрепления пройденного предлагаем решить нижеследующие задачи.
Задача 1. Оцените эффективность проекта на основе данных табл. П.1.10 при Е, равном: а) 0,4; б) 0,3; в) 0,5. Увеличится или уменьшится ЧДД при изменении Е?

Таблица П. 1.10

Задача 2. Оцените эффективность проекта на основе данных табл. П. 1.11. Выполните анализ изменения ЧДД при условии, что Ена 7-м и последующих шагах расчета не превышает 40 %.

Таблица П. 1.11

Задача 3. Оцените эффективность проекта на основе данных табл. П. 1.12 при Е= 0,3. Определите ЧДД си эффективность проекта при условии увеличения (уменьшения) Ktна каждом шаге на 20 %.

Таблица П. 1.12

Задача 4. Рассчитайте эффективность проекта на основе данных табл. П. 1.13. Оцените влияние увеличения Ей продолжительности проекта на ИД и ЧДД.

Таблица П. 1.13

Задача 5. Определите, какому проекту следует отдать предпочтение на основании данных таблиц П.1.14 и П.1.15.

Таблица П. 1.14

Таблица П. 1.15

При получении отрицательных значений ЧДД определите для проектов ВНД, построив график, аналогичный тому, что показан на рис. П. 1.2.

Представьте себе, что эффективность инвестиционных проектов, данные о которых приведены в табл. П.1.14-П.1.15, не устраивает разработчиков проектов. Какие мероприятия необходимо им порекомендовать в целях уменьшения Rt, Зt,, T?
Задача 6. Определите ожидаемый результат в t-мгоду и его вероятность в соответствии с данными табл. П. 1.16.
Задача 7. Определить общий риск инвестиционных проектов, исходные данные которых приведены втабл.П. 1.17-П. 1.19.

Таблица П. 1.16

Таблица П. 1.17

Таблица П. 1.18

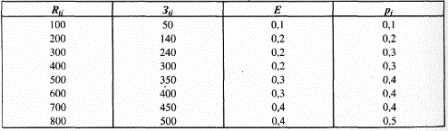
Таблица П. 1.19

3. Простейшие методы оценки целесообразности инвестиций

Среди простых методов определения целесообразности помещения капитала в инвестиционный проект чаще всего используются два — расчет простой нормы прибыли и расчет срока окупаемости.
Отличие простой нормы прибыли ППП от коэффициентов индекса доходности заключается в том, что ее рассчитывают как отношение чистой прибыли ЧП за один какой-либо промежуток времени (обычно за год) к общему объему инвестиций К:

Формулу чистой прибыли можно записать как:

где Ц — общий объем выручки от реализации продукции или услуг (за вычетом НДС); С — издержки производства (себестоимость продукции); Н — налог на прибыль.
В свою очередь, себестоимость продукции:

где И — себестоимость продукции за вычетом амортизационных отчислений (А) и финансовых издержек (платы за кредит) ФИ.
Если значение С из формулы (П. 1.28) подставить в формулу (П. 1.26), то получим:

или

где И — себестоимость продукции (услуг) за вычетом амортизации, но с учетом финансовых издержек; П — прибыль от ценных бумаг.
Экономический смысл простой нормы прибыли заключается в оценке того, какая часть инвестиционных затрат возмещается (возвращается) в виде прибыли в течение одного интервала планирования. Сравнивая расчетное значение ПНП с минимальным или средним уровнем доходности, потенциальный инвестор может прийти к предварительному заключению о целесообразности дальнейшего анализа и проработки инвестиционного проекта.
Необходимо отметить, что поскольку указанный метод предполагает использование данных за каждый год, то бывает трудно, а порой просто невозможно выбрать год, наиболее характерный для проекта. Помимо специфики стадий освоения производства, особенно начальных, и выплаты процентов за кредиты, существуют и некоторые другие факторы, вызывающие изменения уровня чистого дохода в определенные годы. Этот недостаток можно устранить путем использования методов дисконтирования.
Несмотря на определенную значимость метода, использование простой нормы прибыли ограничено сроком окупаемости проекта и непригодно для сопоставления вариантов проектов, различающихся сроками осуществления.
Несколько более сложным является расчет срока окупаемости, или периода возмещения (англ. pay-backperiod). Назначение метода состоит в определении продолжительности периода, в течение которого проект будет работать «на себя». Весь объем приносимых проектом денежных средств, к которым относятся прибыль и амортизационные отчисления, засчитывается как возврат первоначального инвестиционного капитала.
Расчет производится путем постепенного, шаг за шагом, вычитания из общего объема капитальных затрат суммы амортизационных отчислений за очередной интервал планирования (как правило — год). Интервал, в котором остаток становится отрицательным, указывает на искомый «срок окупаемости».
Если такой интервал не выявлен, значит срок окупаемости превышает установленный «срок жизни» проекта.
Определение срока окупаемости в силу наглядности иногда используют как простой метод оценки риска инвестирования.
Срок окупаемости в самом общем виде можно определить по формуле:

Представим себе, что имеется некоторый инвестиционный проект, реализация которого позволит выпускать продукцию объемом 2480 млн руб. При этом издержки производства составляют: И = 1000 млн руб., ФИ = 40 млн руб., П = 80 млн руб., А = 20 млн руб.
Используя формулу (П.1.30), находим:

где К = И - ФИ - А = 1000 - 20 - 40 - 940 млн руб.
Следовательно, на 1 млн руб. вложенных средств можно получить отдачу в размере 1,57 млн руб. Проект можно считать эффективным.
Для закрепления материала предлагаем определить эффективность проектов, условия реализации которых представлены в табл. П.1.20—П.1.23, а также рассчитать срок окупаемости проектов, проанализировав изменение Т0в зависимости от К и прибыли, получаемой в течение «срока жизни» проекта.

Таблица П. 1.20

Таблица П. 1.21

Таблица П. 1.22

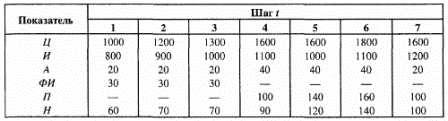
Таблица П. 1.23

.

Ваш комментарий о книге
Обратно в раздел Экономика и менеджмент