Библиотека
Теология
Конфессии
Иностранные языки
Другие проекты
|
Ваш комментарий о книге
Бирюков С., Чередов А. Метрология: Тексты лекций
2. ВИДЫ И МЕТОДЫ ИЗМЕРЕНИЙ
Прежде чем разбираться в сущности каких-либо явлений, удобно их сначала упорядочить, т.е. классифицировать.
Измерения подразделяются на виды измерений – часть области измерений,
имеющая свои особенности и отличающаяся однородностью измеряемых величин, и методы измерений - часть области измерений, состоящая в различии приемов использования принципов и средств измерений.
- Классификация видов измерений
Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующие: способ нахождения численного значения физической величины, число наблюдений, характер зависимости измеряемой величины от времени, число измеряемых мгновенных значений в заданном интервале времени, условия, определяющие точность результатов, способ выражения результатов измерения (рис. 2.1) [7].
По способу нахождения численного значения физической величины измерения подразделяются на следующие виды: прямые, косвенные, совокупные и совместные.
Прямым измерением называют измерение, при котором значение измеряемой физической величины находят непосредственно из опытных данных. Прямые измерения характеризуются тем, что эксперимент как процесс измерения производится над самой измеряемом величиной, имея в виду то или
иное её проявление. Прямые измерения выполняются при помощи средств, предназначенных для измерения данных величин. Числовое значение измеряемой величины отсчитывается непосредственно по показанию измерительного прибора. средств, величин. Примеры прямых измерений: измерение тока амперметром; напряжения - компенсатором; массы - на рычажных весах и др.
Зависимость между измеряемой величиной X и результатом измерения Y при прямом измерении характеризуется уравнением X = Y, т.е. значение измеряемой величины принимается равным полученному результату.
К сожалению, прямое измерение не всегда можно провести. Иногда нет под рукой соответствующего измерительного прибора, или он неудовлетворяет.

по точности, или даже вообще ещё не создан. В этом случае приходится прибегать к косвенному измерению.
Косвенными измерениями называют такие измерения, при которых значение искомой величины находят на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. При косвенных измерениях измеряют не собственно определяемую величину, а другие величины, функционально с ней связанные. Значение измеряемой косвенным путем величины X находят вычислением по формуле
X = F(Y1, Y2, … ,Yn),
где Y1 , Y2 , … Yn - значения величин, полученных путем прямых измерений.
Примером косвенного измерения является определение электрического сопротивления с помощью амперметра и вольтметра. Здесь путем прямых измерений находят значения падения напряжения U на сопротивлении R и ток I через него, а искомое сопротивление R находят по формуле
R = U/I .
Операцию вычисления измеряемой величины может производить вручную или с помощью вычислительного устройства, помещенного в прибор.
Прямые и косвенные измерения в настоящее время широко используются на практике и являются наиболее распространенными видами измерений .
Совокупные измерения - это производимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.
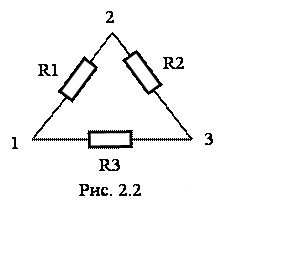 Например, для определения значений сопротивлений резисторов, соединенных треугольником (рис. 2.2), измеряют сопротивления на каждой Например, для определения значений сопротивлений резисторов, соединенных треугольником (рис. 2.2), измеряют сопротивления на каждой
паре вершин треугольника и получают систему уравнений
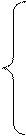 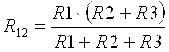 ; ;
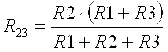 ; ;
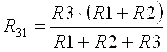 . .
Из решения этой системы уравнений получают значения сопротивлений
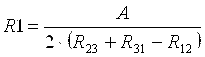 , ,  , , 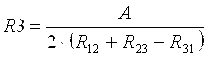 , ,
где 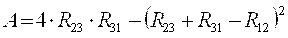 . .
Совместные измерения - это производимые одновременно измерения двух или нескольких неодноименных величин X1, X2,…,Xn, значения которых находят решением системы уравнений:
Fi(X1, X2, … ,Xn; Yi1, Yi2, … ,Yim) = 0,
где i = 1, 2, …, m > n; Yi1, Yi2, … ,Yim - результаты прямых или косвенных измерений; X1, X2, … ,Xn – значения искомых величин.
Например, индуктивность катушки L = L0×(1 + w2×C×L0), где L0 – индуктивность при частоте w = 2×p×f , стремящейся к нулю; С – межвитковая емкость. Значения L0 и С нельзя найти прямыми или косвенными измерениями. Поэтому в простейшем случае измеряют L1 при w1 , а затем L2 при w2 и составляют систему уравнений:
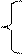 L1 = L0×(1 + w12×C×L0); L1 = L0×(1 + w12×C×L0);
L2 = L0×(1 + w22×C×L0),
решая которую, находят искомые значения индуктивности L0 и емкости С:
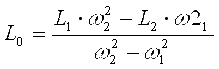 ; ; 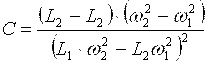 . .
Совокупные и совместные измерения есть обобщение косвенных измерений на случай нескольких величин.
Для повышения точности совокупных и совместных измерений обеспечивают условие m ³ n, т.е. число уравнений должно быть больше или равно числу искомых величин. Получающуюся при этом несовместную систему уравнений решают методом наименьших квадратов.
По числу наблюдений измерения подразделяются на (рис.2.1):
- обыкновенные измерения - измерения, выполняемые с однократным наблюдением;
- статистические измерения - измерения с многократными наблюдениями.
Наблюдение при измерении - экспериментальная операция, выполняемая в процессе измерений, в результате которой получают одно значение из группы значений величин, подлежащих совместной обработке для получения результатов измерений.
Результат наблюдения - результат величины, получаемый при отдельном наблюдении.
По характеру зависимости измеряемой величины от времени измерения разделяются:
- на статические, при которых измеряемая величина остается постоянной во времени в процессе измерения;
- динамические, при которых измеряемая величина изменяется в процессе измерения и является непостоянной во времени.
При динамических измерениях для получения результата измерения необходимо учитывать это изменение. А для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений [1].
По числу измеряемых мгновенных значений в заданном интервале времени измерения подразделяются на дискретные и непрерывные (аналоговые).
Дискретные измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений конечно.
Непрерывные (аналоговые) измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений бесконечно.
По условиям, определяющим точность результатов, измерения бывают:
- максимально возможной точности, достигаемой при существующем уровне техники;
- контрольно-поверочные, погрешность которых не должна превышать
некоторое заданное значение;
- технические, в которых погрешность результата определяется характеристиками средств измерений [11].
По способу выражения результатов измерения различают абсолютные и относительные измерения.
Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.
Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную [12].
2.2. Методы измерений и их классификация
Все измерения могут производиться различными методами. Различают следующие основные методы измерений: метод непосредственной оценки и методы сравнения cмерой [7] .
2.2.1. Метод непосредственной оценки характеризуется тем, что значение измеряемой величины определяется непосредственно по отсчетному устройству измерительного прибора, заранее градуированного в единицах измеряемой величины. Этот метод является наиболее простым и поэтому широко применяется при измерении различных величин, например: измерение веса тела на пружинных весах, силы электрического тока стрелочным амперметром, разности фаз цифровым фазометром и т.д.

Функциональная схема измерения методом непосредственной оценки приведена на рис. 2.3.
Приборы непосредственной оценки всегда содержат измерительный преобразователь, который преобразует измеряемую величину в другую, доступную для сравнения наблюдателем или автоматическим устройством. Так, в стрелочных приборах происходит преобразование измеряемой величины в угол поворота подвижной части, который отмечается стрелкой. По положению стрелки, т.е. сравнением угла поворота с делениями на шкале находится значение измеряемой величины. Мерой в приборах непосредственной оценки служат деления шкалы отсчетного устройства. Они поставлены не произвольно, а на основании градуировки прибора. Градуировка прибора непосредственной оценки состоит в том, что на его вход от меры подается величина заданного размера и отмечается показание прибора. Этому показанию затем присваивается значение известной величины. Таким образом, деления шкалы отсчетного устройства являются как бы заменителем («отпечатком») значения реальной физической величины и поэтому могут быть использованы непосредственно для нахождения значений измеряемых прибором величин. Следовательно, все приборы непосредственной оценки фактически реализуют принцип сравнения с физическими величинами. Но это сравнение разновременное и осуществляется опосредованно, с помощью промежуточного средства – делений шкалы отсчетного устройства.
2.2.2. Методы сравнения с мерой – методы измерений, в которых известную величину сравнивают с величиной, воспроизводимой мерой. Эти методы по сравнению с методом непосредственной оценки более точны, но несколько сложны. Группа методов сравнения с мерой включает в себя следующие методы: противопоставления, нулевой, дифференциальный, совпадения и замещения.
Определяющим признаком методов сравнения является то, что в процессе каждого измерительного эксперимента происходит сравнение двух однородных независимых друг от друга величин - известной (воспроизводимой мерой) и измеряемой. При измерениях методами сравнения используются реальные физические меры, а не их «отпечатки».
Сравнение может быть одновременным, когда мера и измеряемая величина воздействуют на измерительный прибор одновременно, и разновременным, когда воздействие измеряемой величины и меры на измерительный прибор разнесено во времени. Кроме того, сравнение может быть непосредственным и опосредованным. В первом случае измеряемая величина и мера непосредственно воздействуют на устройство сравнения, а во втором – через другие величины, однозначно связанные с известной и измеряемой величинами.
Одновременное сравнение осуществляется обычно методами противопоставления, нулевым, дифференциальным и совпадения, а разновременное - методом замещения.
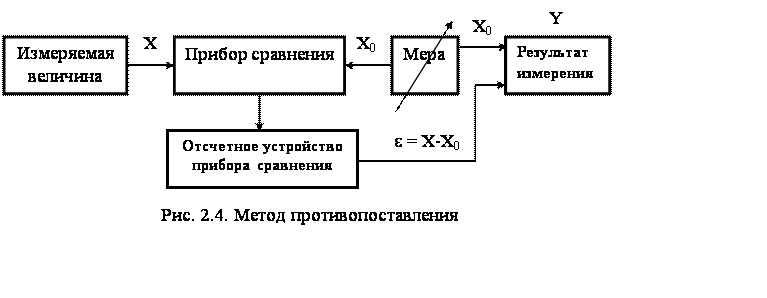
Метод противопоставления – метод сравнения с мерой в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами [2]. Функциональная схема метода противоставления приведена на рис. 2.4.
В этом методе измеряемая величина Х и мера Х0 воздействуют на два входа прибора сравнения. Результирующий эффект воздействия определяется разностью этих величин, т.е. e = Х - Х0 и снимается с отсчетного устройства прибора сравнения. Результат измерения находят как
Y = X0 + e .
Этот метод удобен, если имеются точная многозначная мера и несложные
устройства сравнения. Примером этого метода является взвешивание груза на равноплечих весах с помещением измеряемой массы и уравновешивающих её гирь на двух чашках весов и с полным уравновешиванием весов. При этом измеряемая масса определяется как сумма массы гирь, её уравновешивающих, и показания по шкале весов. Метод противопоставления позволяет значительно уменьшить воздействие на результат измерений влияющих величин, поскольку последние более или менее одинаково искажают сигналы как в цепи преобразования измеряемой величины, так и в цепи преобразования величины, воспроизводимой мерой. Отсчетное устройство прибора сравнения реагирует на разность сигналов, вследствие чего эти искажения в некоторой степени компенсируют друг друга. Этот метод также применяют при измерении ЭДС, напряжения, тока и сопротивления [1].
Нулевой метод является разновидностью метода противопоставления, в котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля. Функциональная схема нулевого метода измерения приведена на рис. 2.5.
Здесь измеряемая величина X и мера X0 воздействуют на два входа измерительного прибора сравнения. Результирующий эффект воздействия определяется разностью этих величин, т.е. e = X – X0 . Изменяя величину, воспроизводимую мерой (это схематически указано на рисунке стрелкой), можно довести величину e до 0. Это обстоятельство отмечается индикатором нуля. Если e = 0, то Х = Хо, результат измерения Y есть полученное значение 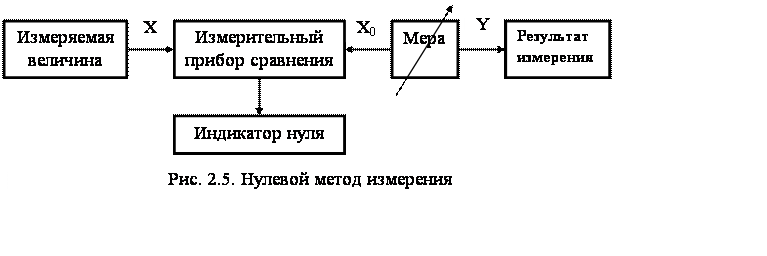 меры, т.е. Y = X0 . меры, т.е. Y = X0 .
Поскольку на индикатор нуля воздействует разность величин, то его предел измерения может быть выбран меньшим, а чувствительность большей, чем у прибора для измерения X методом непосредственной оценки. Точность индикации равенства двух величин может быть весьма большой. А это ведет к повышению точности измерения. Погрешность измерения нулевым методом определяется погрешностью меры и погрешностью индикации нуля. Вторая составляющая обычно много меньше первой, практически точность измерения нулевым методом равна точности меры.
Примерами нулевых методов измерений являются: измерение массы на равноплечих весах с помещением измеряемой массы и уравновешивающих её гирь на двух чашках весов и полным уравновешиванием весов или измерение напряжения путем компенсации его напряжением образцового источника (в обоих случаях осуществляется непосредственное сравнение); а также измерение электрического сопротивления мостом с полным его уравновешиванием (опосредованное сравнение).
Нулевой метод измерения требует обязательного применения многозначных мер. Точность таких мер всегда хуже однозначных мер, кроме того, мы можем не иметь меры переменной величины. В таком случае нулевой метод не применим.
Дифференциальный метод представляет собой метод сравнения с мерой, в котором на измерительный прибор (обязательно прибор сравнения) воздействует разность измеряемой величины и известной величины, воспроизводимой мерой, причем эта разность не доводится до нуля, а измеряется измерительным прибором прямого действия.
На рис. 2.6 показана функциональная схема дифференциального метода.
Здесь мера имеет постоянное значение Х0, разность измеряемой величины Х и меры Х0, т.е. e = Х - Х0, не равна нулю и измеряется измерительным прибором. Результат измерения находятся как
Y = X0 + e .

То обстоятельство, что здесь измерительный прибор измеряет не всю величину Х, а только её часть e, позволяет уменьшить влияние на результат измерения погрешности измерительного прибора, причем влияние погрешности измерительного прибора тем меньше, чем меньше разность e .
Действительно, при измерении напряжения U = 97 В вольтметром непосредственной оценки с пределом измерения 100 В и допущенной относительной погрешности измерения этого напряжения 1 % (0,01) мы получаем абсолютную погрешность измерения D1 = 97×0,01 = 0,97 » 1 В. Если же будем измерять это напряжение дифференциальным методом с использованием образцового источника напряжения U0 = 100 В, то разность напряжений U – U0 = (97 - 100)В = - 3 В мы можем измерить вольтметром с пределом измерения всего 3 В. Пусть относительная погрешность измерения этого напряжения будет также равна 1 % . Это даёт абсолютную погрешность измерения напряжения 3 В: D2 = 3×0,01 = 0,03 В . Если эту погрешность привести к измеряемому напряжению U , мы получим относительную погрешность измерения напряжения: D2/U = 0,03/97 » 0,0003 (0,03 %), т.е. приблизительно в 30 раз меньше, чем при измерении напряжения U методом непосредственной оценки. Это увеличение точности измерения произошло потому, что в первом случае прибором была измерена почти вся величина с относительной погрешностью в 1 % , а во втором случае измеряется не вся величина, а только её 1/30 часть.
В этих расчетах не учитывалась погрешность меры, которая полностью входит в результат измерения. Следовательно, при малых разностных величинах e точность измерения дифференциальным методом приближается к точности измерения нулевым методом и определяется лишь погрешностью меры. Кроме того, дифференциальный метод не требует меры переменной величины.
В приведенном выше примере измерения напряжения дифференциальным методом использовалось непосредственное сравнение.
Другим примером дифференциального метода измерения может служить определение отклонения сопротивления резистора от номинала неуравновешенным (процентным) мостом (здесь реализуется опосредованное сравнение).
Метод совпадений (или метод «нониуса») представляет собой метод сравнения с мерой, в котором разность между измеряемой величиной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.
Этот метод применяется в тех случаях, когда измеряемая величина меньше цены деления заданной меры. При этом применяются две меры с разными ценами деления, которые отличаются на размер оцениваемого разряда отсчетов.
Пусть имеем одну калиброванную меру с ценой деления Dxk1 и измеряемую величину Dx, которая меньше цены деления. В этом случае используют вторую меру с ценой деления Dxk2 . Таким образом, если чувствительность необходимо увеличить в п раз, то соотношение между ними будет иметь вид
Dxk2 = Dxk1×(1 - 1/n).
В частности, при n = 10 Dxk2 =0,9 ×Dxk1 .
Измеряемую величину Dx устанавливают между нулевыми отметками мер и находят число Nx, равное номеру совпавших делений мер (рис. 2.7). В этом случае справедливо соотношение Nx×Dxk1 = Dx + Nx×Dxk2 , откуда
Dx = Nx×( Dxk1 - Dxk2) = Nx×(Dxk1 – 0,9×Dxk1) = Nx×0,1×Dxk1 .
Примером измерения методом совпадения может служить измерение длины детали с помощью штангенциркуля с нониусом, другим примером - измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по частоте вспышек и смещению метки определяют частоту вращения детали. Метод "нониуса" находит также широкое применение при измерении временных интервалов двух близких частот (биений) и в других случаях [5].

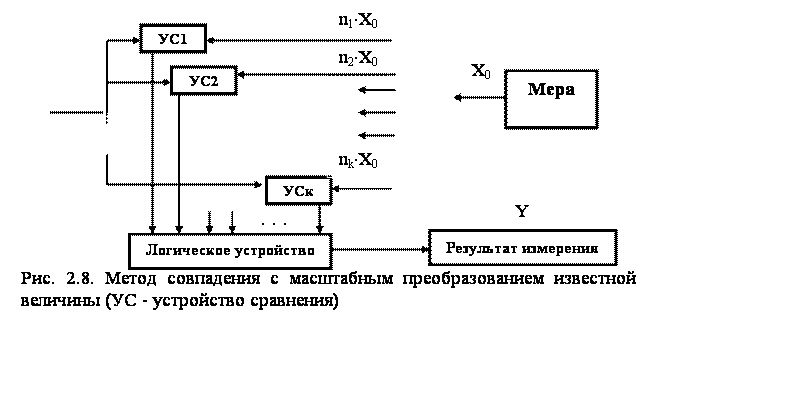
Функциональная схема прибора, работающего по методу совпадений с масштабным преобразованием только величины, воспроизводимой мерой, показана на рис. 2.8. Здесь величина X0 однозначной меры подвергается масштабному преобразованию для выработки величин n1X0, n2X0, … njX0, … nkX0, Эти величина подаются на k- устройств сравнения, к ним же прикладывается и измеряемая величина Х. Логическое устройство указывает номер устройства сравнения, у которого Х - njX0 = min и определяет измеряемую величину на основе приближенного соотношения X = njX0. Такой метод измерения нашел применение также в цифровых приборах, измеряющих угловые и линейные перемещения. Метод совпадения требует наличия многозначных мер или масштабных преобразователей величины и величины, воспроизводимой мерой. Поэтому в измерительной технике он используется сравнительно редко.
Метод замещения есть метод сравнения с мерой, в котором измеряемую величину замещают известной величиной, воспроизводимой мерой [2].
Функциональная схема метода замещения изображена на рис. 2.9. В нем используется измерительный прибор непосредственной оценки.
     Техника измерения состоит в следующем. Сначала на вход измерительного прибора подают измеряемую величину Х и отмечают показания прибора (отсчет) Y1 . После этого вместо измеряемой величины на тот же самый Техника измерения состоит в следующем. Сначала на вход измерительного прибора подают измеряемую величину Х и отмечают показания прибора (отсчет) Y1 . После этого вместо измеряемой величины на тот же самый
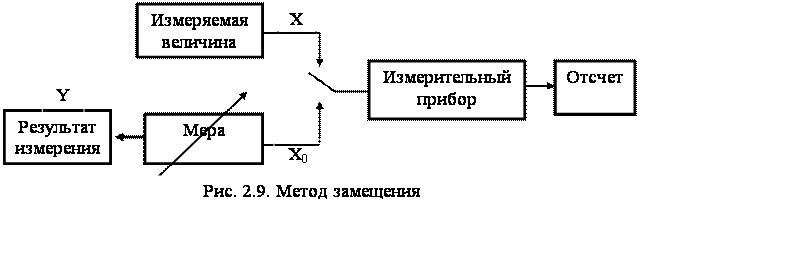
вход (это очень существенно) прибора подают величину Х0, воспроизводимую мерой. В этом случае показание прибора становится равным Y2. Изменяя величину, воспроизводимую мерой, добиваются равенства показаний, т.е. Y1= Y2 . При этом можно утверждать, что Х = Х0 независимо от погрешности измерительного прибора. Действительно, в первом случае получаем Y1= X + D1,
где D1 - погрешность измерительного прибора при получении отсчета Y1 .
При воздействии на прибор меры Y2= X + D2. Здесь D2 - погрешность измерительного прибора при получении отсчета Y2.
Поскольку мы добиваемся одинаковых показаний ( Y1 = Y2 ), а интервал времени между двумя измерениями невелик, то на одной и той же отметке шкалы прибора погрешность одинакова, т.е. D1 = D2 . Следовательно, из равенства Y1 = Y2 или X + D1 = X + D2 вытекает, что Х = Х0.
Исключение погрешности измерительного прибора из результата измерений является новым достоинством метода замещения. В нулевом методе измерения погрешность измерительного прибора проявляет себя тем, что нулевое показание может не соответствовать равенству измеряемой величины и меры, а в дифференциальном методе она представляет собой погрешность измерения разности меры и измеряемой величины. Для получения большой точности измерения нулевым и дифференциальным методом необходимо, чтобы погрешности измерительных приборов были невелики. А вот метод замещения не требует этого условия! Даже если погрешность измерительного прибора достаточно велика, это не скажется на результате измерения. Таким образом, методом замещения можно осуществить точное измерение, имея прибор с большой погрешностью. Нетрудно сообразить, что точность измерения методом замещения определяется погрешностью меры. Правда, при более строгом подходе к методу замещения следует учитывать два обстоятельства.
Во-первых, здесь сравнение разновременное, а за время между двумя измерениями погрешность измерительного прибора может несколько измениться, так что равенство D1 = D2 несколько нарушится. Теперь становится ясно, почему измеряемая величина и мера должны подаваться на один и тот же вход прибора. Это прежде всего связано с тем, что погрешность измерительного прибора на разных входах даже при одинаковых показаниях может быть разной!
Во-вторых, метод замещения сводится к получению одинаковых показаний прибора. Само равенство показаний может быть установлено с конечной точностью. А это также ведет к погрешности измерения. Точность установления равенства показаний будет больше в приборе, обладающем большей чувствительностью.
Следовательно, при измерении методом замещения следует использовать не точный, но чувствительный и быстродействующий прибор. Тогда остаточная погрешность, обусловленная измерительным прибором, будет невелика.
Метод замещения является самым точным из всех известных методов и обычно используется для проведения наиболее точных (прецизионных) измерений. Ярким примером метода замещения является взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (вспомните - на один и тот же вход прибора). Известно, что таким методом можно правильно измерить массу тела, имея неверные весы (погрешность прибора), но никак не гири! (погрешность меры).
Сравнивая между собой метод замещения и метод непосредственной оценки, мы обнаружим их разительное сходство. Действительно, метод непосредственной оценки по своей сути представляет метод замещения. Почему он выделен в отдельный метод? Все дело в том, что при измерении методом непосредственной оценки мы выполняем только первую операцию - определение показаний. Вторая операция - градуировка (сравнение с мерой) производится не при каждом измерении, а лишь в процессе производства прибора и его периодических поверках. Между применением прибора и его предыдущей поверкой может лежать большой интервал времени, а погрешность измерительного прибора за это время может значительно измениться. Это и приводит к тому, что метод непосредственной оценки дает обычно меньшую точность измерения, чем метод сравнения [7].
Рассмотренная классификация методов измерений изображена на рис. 2.10.
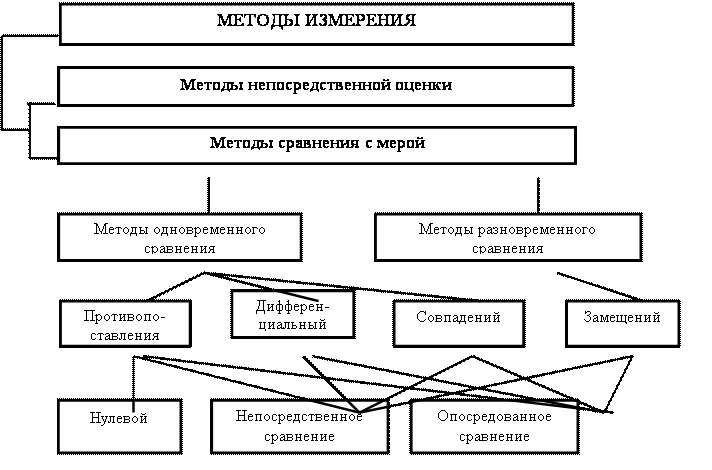
Рис. 2.10. Классификация методов измерений
Рассмотренные методы определяют принципы построения измерительных приборов. Их не следует путать с методикой измерения и алгоритмом измерения.
Методика измерений - детально намеченный порядок процесса измерений, регламентирующий методы, средства, алгоритмы выполнения измерений, которые в определенных (нормированных) условиях обеспечивают измерения с заданной точностью.
Измерения должны осуществляться в соответствии с аттестованными в установленном порядке методиками. Порядок разработки и аттестации методик выполнения измерений определяется Госстандартом России.
Алгоритм измерения - точное предписание о выполнении в определенном порядке совокупности операций, обеспечивающих измерение значения физической величины.
.
Ваш комментарий о книге
Обратно в раздел Наука
|
|
